Les algorithmes de tri des éléments d'un tableau ont une place à part en algorithmique. En effet, ils sont souvent utilisés pour mettre en évidence certains concepts algorithmiques (concepts que l'on retrouve dans d'autres types d'algorithmes). Nous allons commencer par un algorithmes "classiques" : le tri par sélection.
Tri par insertion
Entrons tout de suite dans le vif du sujet, voici l'algorithme du tri par insertion :
VARIABLE
t : tableau d'entiers
i : nombre entier
j : nombre entier
k : nombre entier
DEBUT
j←2
tant que j<=longueur(t): //boucle 1
i←j-1
k←t[j]
tant que i>0 et que t[i]>k: //boucle 2
t[i+1]←t[i]
i←i-1
fin tant que
t[i+1]←k
j←j+1
fin tant que
FIN
Remarque : il est possible de mettre des commentaires à l'aide de "//" afin de rendre la compréhension des algorithmes plus aisée
À faire vous-même 1
Poursuivez le travail commencé ci-dessous (attention de bien donner l'état du tableau à chaque étape)
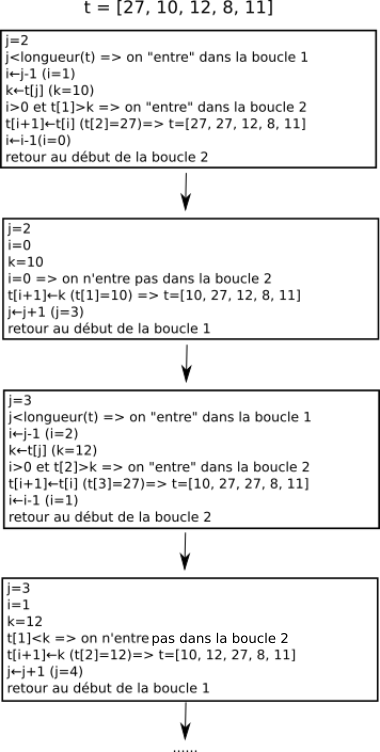
On peut résumer le principe de fonctionnement de l'algorithme de tri par insertion avec le schéma suivant :
À faire vous-même 2
Essayez de produire le même type de schéma explicatif que ci-dessus avec le tableau t = [12, 8, 23, 10, 15]
Essayons maintenant de déterminer la complexité de l'algorithme de tri par insertion :
Comme précédemment nous nous intéresserons à la complexité en temps dans le pire des cas. À quoi correspond le pire des cas pour un algorithme de tri ? Tout simplement quand le tableau initial est "trié à l'envers" (les entiers sont classés du plus grand au plus petit), comme dans cet exemple : t = [5, 4, 3, 2, 1].
Pour déterminer la complexité de l'algorithme de tri par insertion nous n'allons pas rechercher le nombre d'opérations élémentaires, mais, pour souci de simplicité, directement nous intéresser au "nombre de décalages effectués" pour trier entièrement un tableau. J'appelle "décalage" ce qui est symbolisé par une flèche noire sur le schéma ci-dessous :
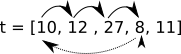
Pour l'étape ci-dessus nous avons 3 décalages (décalages du 10, du 12 et du 27). Nous ne tiendrons pas compte du "placement" du nombre en cours de traitement (8 dans notre exemple) symbolisé par la flèche en pointillé.
Évaluons le nombre de décalages nécessaires pour trier le tableau t = [5, 4, 3, 2, 1]
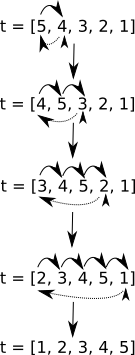
Il est, je l'espère, évident pour vous que nous avons : 1 + 2 + 3 + 4 = 10 décalages.
Dans le cas où nous avons un tableau à trier qui contient n éléments, nous aurons : 1 + 2 + 3 +....+ n-3 + n-2 + n-1 décalages (puisque pour 5 éléments nous avons 1 + 2 + 3 + 4 ). Si vous n'êtes pas convaincu, faites le test avec un tableau de 6 éléments, vous devriez trouver 1 + 2 + 3 + 4 + 5 = 15 décalages.
Que vaut cette somme S = 1 + 2 + 3 + .... + n-3 + n-2 + n-1 ?
Écrivons cette somme un peu différemment : S' = n-1 + n-2 + n-3 + .... + 3 + 2 + 1 (avec S = S' puisque l'addition est commutative)
En associant les termes de cette somme un par un nous obtenons : S + S' = n + n + n + .... + n + n + n (puisque 1+n-1=n, 2+n-2=n, 3+n-3=n,...., n-3+3=n, n-2+2=n et n-1+1=n)
Soit, puisque S=S' : 2S = n + n + n + .... + n + n + n
Si vous comptez bien nous avons n-1 fois n, ce que l'on peut écrire : 2S = $n(n-1)$ soit S = $\frac{n(n-1)}{2}$ soit S = $\frac{n^2-n}{2}$ soit encore S = $\frac{1}{2}n^2-\frac{1}{2}n$
Comme nous l'avons vu précédemment $\frac{1}{2}n^2-\frac{1}{2}n$ = O($n^2$), l'algorithme de tri par insertion a donc une complexité en O($n^2$). On parle aussi de complexité quadratique.
Passons maintenant à un autre algorithme de tri : le tri par sélection
Tri par sélection
VARIABLE
t : tableau d'entiers
i : nombre entier
min : nombre entier
j : nombre entier
DEBUT
i←1
tant que i<longueur(t): //boucle 1
j←i+1
min←i
tant que j<=longueur(t): //boucle 2
si t[j]<t[min]:
min←j
fin si
j←j+1
fin tant que
si min≠i :
échanger t[i] et t[min]
fin si
i←i+1
fin tant que
FIN
À faire vous-même 3
Poursuivez le travail commencé ci-dessous (attention de bien donner l'état du tableau)
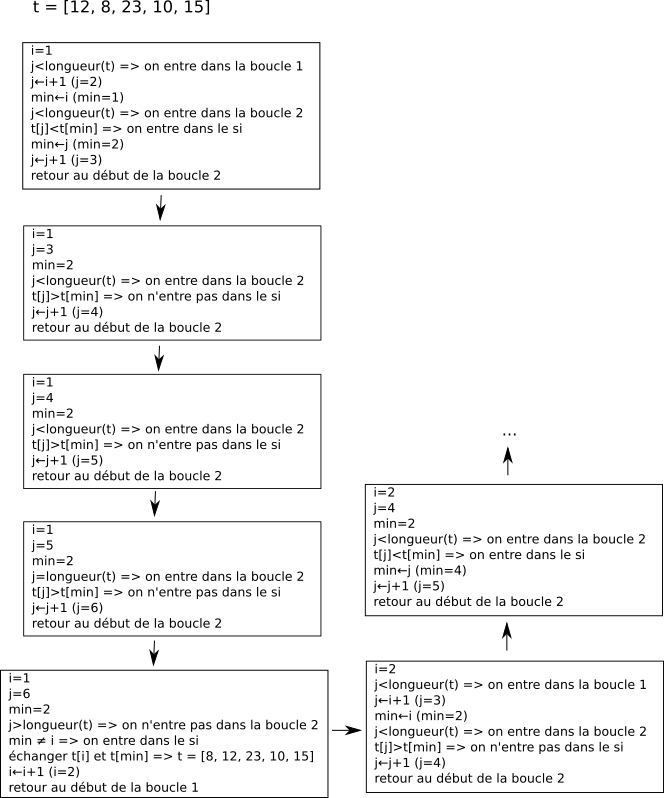
On peut résumer le principe de fonctionnement de l'algorithme de tri par sélection avec le schéma suivant :

À faire vous-même 4
Essayez de produire le même type de schéma explicatif que ci-dessus avec le tableau t = [12, 8, 23, 10, 15]
Essayons maintenant de déterminer la complexité de l'algorithme de tri par sélection :
Pour établir la complexité de cet algorithme, nous n'allons pas directement nous intéresser au nombre d'opérations élémentaires. Nous allons comptabiliser les comparaisons entre 2 entiers.
Si nous nous intéressons à l'étape qui nous permet de passer de t = [12, 8, 23, 10, 15] à t = [8, 12, 23, 10, 15] (i = 1) nous avons 4 comparaisons : 12 avec 8, puis 8 avec 23, puis 8 avec 10 et enfin 8 avec 15.
Si nous nous intéressons à l'étape qui nous permet de passer de t = [8, 12, 23, 10, 15] à t = [8, 10, 23, 12, 15] (i = 2) nous avons 3 comparaisons : 12 avec 23, puis 12 avec 10, et enfin 10 avec 15.
Si nous nous intéressons à l'étape qui nous permet de passer de t = [8, 10, 23, 12, 15] à t = [8, 10, 12, 23, 15] (i = 3) nous avons 2 comparaisons : 23 avec 12 et 12 avec 15
Si nous nous intéressons à l'étape qui nous permet de passer de t = [8, 10, 12, 23, 15] à t = [8, 10, 12, 15, 23] (i = 4) nous avons 1 comparaison : 23 avec 15
Pour trier un tableau comportant 5 éléments nous avons : 4 + 3 + 2 + 1 = 10 comparaisons
Dans le cas où nous avons un tableau à trier qui contient n éléments, nous aurons : n-1 + n-2 + n-3 +....+ 3 + 2 + 1 comparaisons. Si vous n'êtes pas convaincu, faites le test avec un tableau de 6 éléments, vous devriez trouver 5 + 4 + 3 + 2 +1 = 15 comparaisons.
Vous avez sans doute déjà remarqué que nous avons un résultat similaire au tri par insertion (sauf que nous nous intéressons ici aux comparaisons alors que pour le tri par insertion nous nous intéressons aux décalages, mais cela ne change rien au problème)
Conclusion : nous allons trouver exactement le même résultat que pour le tri par insertion : l'algorithme de tri par sélection a une complexité en O($n^2$) (complexité quadratique).
Nous avons vu précédemment des algorithmes de complexité linéaire ($O(n)$) avec les algorithmes de recherche d'un entier dans un tableau, de recherche d'un extremum ou encore de calcul d'une moyenne. Nous avons vu ici que les algorithmes de tri par sélection et de tri par insertion ont tous les deux une complexité quadratique ($O(n^2)$). Il est important de bien avoir conscience de l'impact de ces complexités sur l'utilisation des algorithmes : si vous doublez la taille du tableau, vous doublerez le temps d'exécution d'un algorithme de complexité linéaire, en revanche vous quadruplerez le temps d'exécution d'un algorithme de complexité quadratique.