Recherche dichotomique

Nous avons déjà eu l'occasion d'étudier un algorithme de recherche d'un entier dans un tableau. Dans le pire des cas (l'entier recherché n'est pas dans le tableau), l'algorithme parcourt l'ensemble du tableau, nous avions donc une complexité O(n). Est-on obligé de parcourir l'ensemble du tableau pour vérifier qu'un entier x ne se trouve pas dans un tableau t ? A priori oui, sauf si le tableau t est trié !

Agorithme de recherche dichotomique


VARIABLE
t : tableau d'entiers trié
mil : nombre entier
fin : nombre entier
deb : nombre entier
x : nombre entier // x : l'entier recherché
tr : booléen
DEBUT
tr ← FAUX
deb ← 1
fin ← longueur(t)
tant que tr == FAUX et que deb ⩽ fin :
 mil ← partie_entière((deb+fin)/2)
 si t[mil] == x :
  tr = vrai
 sinon :
  si x > t[mil] :
   deb ← mil+1
  sinon :
   fin ← mil-1
  fin si
 fin si
fin tant que
renvoyer la valeur de tr
FIN

À faire vous-même 1

Étudier attentivement l'analyse effectuée ci-dessous :

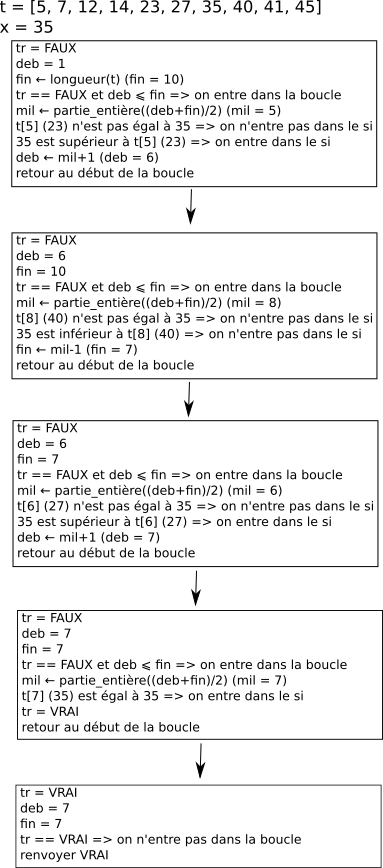
On peut résumer le principe de fonctionnement de l'algorithme de recherche dichotomique par le schéma suivant :

schéma 1

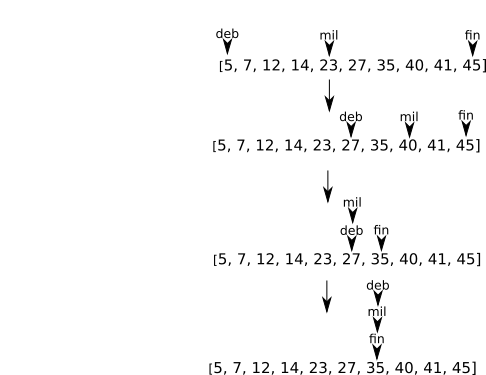
Il est aussi possible de représenter le principe de l'algorithme de recherche dichotomique avec le schéma suivant :

schéma 2

L'idée est donc de définir le milieu du tableau (variable "mil") et de couper le tableau en 2, on se retrouve avec 2 tableaux. On garde uniquement le tableau qui peut contenir la valeur recherchée. On recommence le processus jusqu'au moment où l'on "tombe" sur la valeur recherchée ou que l'on se retrouve avec un tableau contenant un seul élément : si l'élément unique du tableau n'est pas l'élément recherché, l'algorithme renvoie FAUX.

À faire vous-même 2

Reproduire l'analyse effectuée au "À faire vous-même 1" avec t = [5, 7, 12, 14, 23, 27, 35, 40, 41, 45] et x = 9

Représentez le principe de fonctionnement de l'algorithme (pour le cas t = [5, 7, 12, 14, 23, 27, 35, 40, 41, 45] et x = 9) à l'aide d'un schéma (le même type que le schéma 2)

À faire vous-même 3

Reproduire l'analyse effectuée au "À faire vous-même 1" avec t = [5, 7, 12, 14, 23, 27, 35, 40, 41, 45] et x = 40

Représentez le principe de fonctionnement de l'algorithme (pour le cas t = [5, 7, 12, 14, 23, 27, 35, 40, 41, 45] et x = 40) à l'aide d'un schéma (le même type que le schéma 2)

Complexité

Pour étudier la complexité, nous allons nous intéresser à la boucle : au niveau de la boucle, combien doit-on effectuer d'itérations pour un tableau de taille n dans le cas le plus défavorable (l'entier x n'est pas dans le tableau t) ?

Sachant qu'à chaque itération de la boucle on divise le tableau en 2, cela revient donc à se demander combien de fois faut-il diviser le tableau en 2 pour obtenir, à la fin, un tableau comportant un seul entier ? Autrement dit, combien de fois faut-il diviser n par 2 pour obtenir 1 ?

Mathématiquement cela se traduit par l'équation $\frac{n}{2^a}=1$ avec a le nombre de fois qu'il faut diviser n par 2 pour obtenir 1. Il faut donc trouver a !

A ce stade il est nécessaire d'introduire une nouvelle notion mathématique : le "logarithme base 2" noté $log_2$. Par définition $log_2(2^x)=x$

Nous avons donc :

$\frac{n}{2^a}=1$ => $n=2^a$ => $log_2(n)=log_2(2^a)=a$, nous avons donc $a=log_2(n)$

Nous pouvons donc dire que la complexité en temps dans le pire des cas de l'algorithme de recherche dichotomique est $O(log_2(n))$

Afin de pouvoir comparer l'efficacité des différents algorithmes, voici une représentation graphique des fonctions $y=x$ (en rouge), $y=x^2$ (en bleu) et $y=log_2(x)$ (en vert)

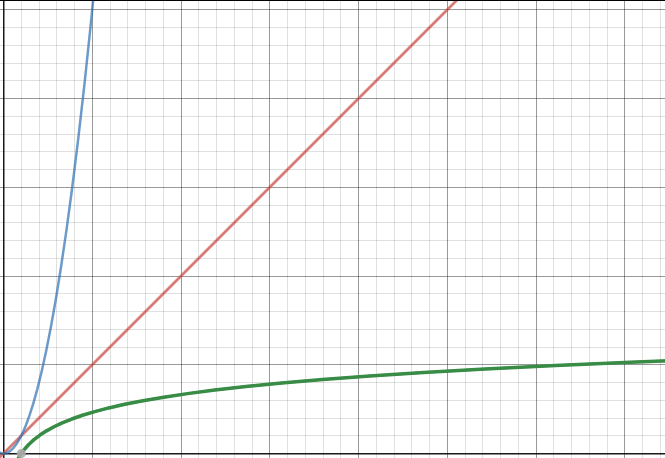
Comme vous pouvez le constater l'algorithme de recherche dichotomique est plus efficace que l'algorithme de recherche qui consiste à parcourir l'ensemble du tableau, car $x>log_2(x)$ quelque soit $x$. Cependant, il ne faut pas perdre de vu que dans le cas de la recherche dichotomique, il est nécessaire d'avoir un tableau trié, si au départ le tableau n'est pas trié, il faut rajouter la durée du tri.

Pour terminer, nous allons démontrer que cet algorithme se termine dans tous les cas (on ne peut pas "tomber dans une boucle infinie") :

Nous avons les variables "fin" et "deb". Définissons fin_i et deb_i avec i qui correspond à la ième itération de la boucle : deb₀ correspond à la valeur de la variable "deb" avant la première itération de la boucle (nous avons donc deb₀ = 0). Même chose pour fin_i (nous avons donc fin₀ = n). À la fin de la première itération de la boucle, nous aurons fin₁ et deb₁... Par exemple, dans l'exemple traité au "À faire vous-même 1", nous avons : deb₀ = 0, fin₀ = 10, deb₁ = 6, fin₁ = 10, deb₂ = 6, fin₂ = 7, deb₃ = 7, fin₃ = 7.

On définit aussi m_i = (deb_i + fin_i) / 2.

Partons du principe que nous sommes à la k ième itération (i=k), nous avons plusieurs cas à considérer :

si deb_k > fin_k ou si t[m_k] = x, l'algorithme se termine, car on "n'entre pas" dans la boucle.
si deb_k ⩽ fin_k et si x < t[m_k], on "entre" dans la boucle : deb_k+1 = deb_k et fin_k+1 = m_k - 1. On a alors fin_k+1 - deb_k+1 < fin_k - deb_k
si deb_k ⩽ fin_k et si x > t[m_k], on "entre" dans la boucle : deb_k+1 = m_k + 1 et fin_k+1 = fin_k. On a alors fin_k+1 - deb_k+1 < fin_k - deb_k

Quel que soit le cas, nous avons fin_k+1 - deb_k+1 < fin_k - deb_k, nous pouvons donc dire que fin_i - deb_i est strictement décroissante. Il existe donc un entier p tel que :

soit deb_p > fin_p, dans ce cas l'algorithme va se terminer, car on "n'entre pas" dans la boucle et l'algorithme renvoie FAUX.
soit x = t[m_p] avec m_p = (deb_p + fin_p) / 2, dans ce cas l'algorithme va se terminer, car on "n'entre pas" dans la boucle et l'algorithme renvoie VRAI.

Nous venons démontrer que l'algorithme se termine à un moment ou à un autre. Pour effectuer cette démonstration nous avons utilisé le fait que fin_i - deb_i est strictement décroissante. "fin_i - deb_i" est appelé un "variant" de boucle. Un variant de boucle est une grandeur qui, comme son nom l'indique, varie à chaque itération, cette variation fait qu'à un moment ou à un autre, l'algorithme finira par s'arrêter.

À faire vous-même 4

Proposez une implémentation en Python de l'algorithme de recherche dichotomique. Vous testerez votre programme avec le tableau t = [5, 7, 12, 14, 23, 27, 35, 40, 41, 45] et l'entier x = 35 puis, toujours avec le même tableau t mais cette fois avec l'entier x = 9

Auteur : David Roche