Algorithmes sur les arbres binaires

Il est conseillé de relire au moins une fois le cours consacré aux arbres.

Avant d'entrer dans le vif du sujet (les algorithmes), nous allons un peu approfondir la notion d'arbre binaire :

À chaque noeud d'un arbre binaire, on associe une clé ("valeur" associée au noeud on peut aussi utiliser le terme "valeur" à la place de clé), un "sous-arbre gauche" et un "sous-arbre droit"

Soit l'arbre binaire suivant :

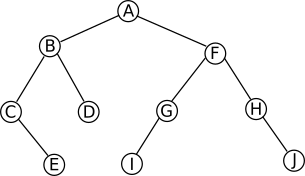
si on prend le noeud ayant pour clé A (le noeud racine de l'arbre) on a :

le sous-arbre gauche est composé du noeud ayant pour clé B, du noeud ayant pour clé C, du noeud ayant pour clé D et du noeud ayant pour clé E
le sous-arbre droit est composé du noeud ayant pour clé F, du noeud ayant pour clé G, du noeud ayant pour clé H, du noeud ayant pour clé I et du noeud ayant pour clé J

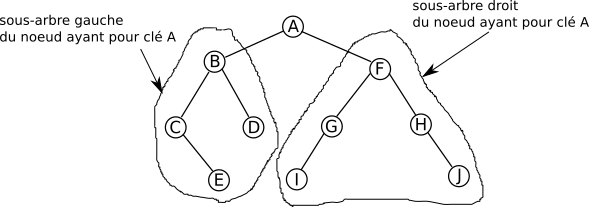
si on prend le noeud ayant pour clé B on a :

le sous-arbre gauche est composé du noeud ayant pour clé C et du noeud ayant pour clé E
le sous-arbre droit est uniquement composé du noeud ayant pour clé D

Un arbre (ou un sous-arbre) vide est noté NIL (NIL est une abréviation du latin nihil qui veut dire "rien")

si on prend le noeud ayant pour clé G on a :

le sous-arbre gauche est uniquement composé du noeud ayant pour clé I
le sous-arbre droit est vide (NIL)

Il faut bien avoir en tête qu'un sous-arbre (droite ou gauche) est un arbre (même s'il contient un seul noeud ou pas de noeud de tout (NIL)).

Soit un arbre T : T.racine correspond au noeud racine de l'arbre T

Soit un noeud x :

x.gauche correspond au sous-arbre gauche du noeud x
x.droit correspond au sous-arbre droit du noeud x
x.clé correspond à la clé du noeud x

Il faut noter que si le noeud x est une feuille, x.gauche et x.droite sont des arbres vides (NIL)

Calculer la hauteur d'un arbre

Nous allons commencer à travailler sur les algorithmes en nous intéressant à l'algorithme qui permet de calculer la hauteur d'un arbre :

À faire vous-même 1

Étudiez cet algorithme :


VARIABLE
T : arbre
x : noeud

DEBUT
HAUTEUR(T) :
  si T ≠ NIL :
    x ← T.racine
    renvoyer 1 + max(HAUTEUR(x.gauche), HAUTEUR(x.droit))
  sinon :
    renvoyer 0
  fin si
FIN

N.B. la fonction max renvoie la plus grande valeur des 2 valeurs passées en paramètre (exemple : max(5,6) renvoie 6)

Cet algorithme est loin d'être simple, n'hésitez pas à écrire votre raisonnement sur une feuille de brouillon. Vous pourrez par exemple essayer d'appliquer cet algorithme sur l'arbre binaire ci-dessous. N'hésitez pas à poser des questions si nécessaire.

Si vraiment vous avez des difficultés à comprendre le fonctionnement de l'algorithme sur l'arbre ci-dessus, vous trouverez ici un petit calcul qui pourrait vous aider.

Comme vous l'avez sans doute remarqué, nous avons dans l'algorithme ci-dessus une fonction récursive. Vous aurez l'occasion de constater que c'est souvent le cas dans les algorithmes qui travaillent sur des structures de données telles que les arbres.

Calculer la taille d'un arbre

Nous allons maintenant étudier un algorithme qui permet de calculer le nombre de noeuds présents dans un arbre.

À faire vous-même 2

Étudiez cet algorithme :


VARIABLE
T : arbre
x : noeud

DEBUT
TAILLE(T) :
  si T ≠ NIL :
    x ← T.racine
    renvoyer 1 + TAILLE(x.gauche) + TAILLE(x.droit)
  sinon :
    renvoyer 0
  fin si
FIN

Cet algorithme ressemble beaucoup à l'algorithme étudié au "À faire vous-même 1", son étude ne devrait donc pas vous poser de problème.

Appliquez cet algorithme à l'exemple suivant :

Il existe plusieurs façons de parcourir un arbre (parcourir un arbre = passer par tous les noeuds), nous allons en étudier quelques-unes :

Parcourir un arbre dans l'ordre infixe

À faire vous-même 3

Étudiez cet algorithme :


VARIABLE
T : arbre
x : noeud

DEBUT
PARCOURS-INFIXE(T) :
  si T ≠ NIL :
    x ← T.racine
    PARCOURS-INFIXE(x.gauche)
    affiche x.clé
    PARCOURS-INFIXE(x.droit)
  fin si
FIN

Vérifiez qu'en applicant l'algorithme ci-dessus, l'arbre ci-dessous est bien parcouru dans l'ordre suivant : C, E, B, D, A, I, G, F, H, J

Parcourir un arbre dans l'ordre préfixe

À faire vous-même 4

Étudiez cet algorithme :


VARIABLE
T : arbre
x : noeud

DEBUT
PARCOURS-PREFIXE(T) :
  si T ≠ NIL :
    x ← T.racine
    affiche x.clé
    PARCOURS-PREFIXE(x.gauche)
    PARCOURS-PREFIXE(x.droit)
  fin si
FIN

Vérifiez qu'en applicant l'algorithme ci-dessus, l'arbre ci-dessous est bien parcouru dans l'ordre suivant : A, B, C, E, D, F, G, I, H, J

Parcourir un arbre dans l'ordre suffixe

À faire vous-même 5

Étudiez cet algorithme :


VARIABLE
T : arbre
x : noeud

DEBUT
PARCOURS-SUFFIXE(T) :
  si T ≠ NIL :
    x ← T.racine
    PARCOURS-SUFFIXE(x.gauche)
    PARCOURS-SUFFIXE(x.droit)
    affiche x.clé
  fin si
FIN

Vérifiez qu'en applicant l'algorithme ci-dessus, l'arbre ci-dessous est bien parcouru dans l'ordre suivant : E, C, D, B, I, G, J, H, F, A

Le choix du parcours infixe, préfixe ou suffixe dépend du problème à traiter, on pourra retenir pour les parcours préfixe et suffixe (le cas du parcours infixe sera traité un peu plus loin) que :

dans le cas du parcours préfixe, un noeud est affiché avant d'aller visiter ces enfants
dans le cas du parcours suffixe, on affiche chaque nœud après avoir affiché chacun de ses fils

Parcourir un arbre en largeur d'abord

À faire vous-même 6

Étudiez cet algorithme :


VARIABLE
T : arbre
Tg : arbre
Td : arbre
x : noeud
f : file (initialement vide)

DEBUT
PARCOURS-LARGEUR(T) :
  enfiler(T.racine, f) //on place la racine dans la file
  tant que f non vide :
    x ← defiler(f)
    affiche x.clé
    si x.gauche ≠ NIL :
      Tg ← x.gauche
      enfiler(Tg.racine, f)
    fin si
    si x.droit ≠ NIL :
      Td ← x.droite
      enfiler(Td.racine, f)
    fin si
  fin tant que
FIN

Vérifiez qu'en applicant l'algorithme ci-dessus, l'arbre ci-dessous est bien parcouru dans l'ordre suivant : A, B, F, C, D, G, H, E, I, J

Selon vous, pourquoi parle-t-on de parcours en largeur ?

Il est important de bien noter l'utilisation d'une file (FIFO) pour cet algorithme de parcours en largeur. Vous noterez aussi que cet algorithme n'utilise pas de fonction récursive.

Arbre binaire de recherche

Un arbre binaire de recherche est un cas particulier d'arbre binaire. Pour avoir un arbre binaire de recherche :

il faut avoir un arbre binaire !
il faut que les clés de noeuds composant l'arbre soient ordonnables (on doit pouvoir classer les noeuds, par exemple, de la plus petite clé à la plus grande)
soit x un noeud d'un arbre binaire de recherche. Si y est un noeud du sous-arbre gauche de x, alors il faut que y.clé ⩽ x.clé. Si y est un noeud du sous-arbre droit de x, il faut alors que x.clé ⩽ y.clé

À faire vous-même 7

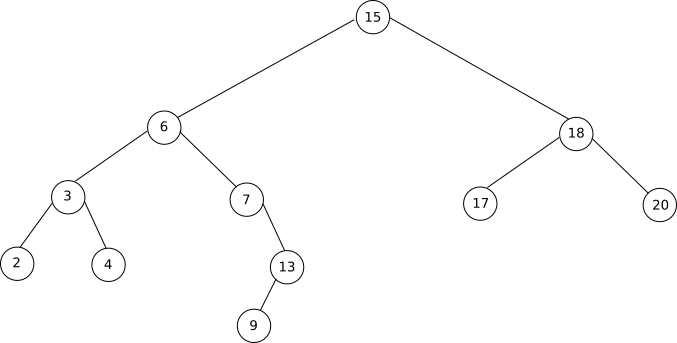
Vérifiez que l'arbre ci-dessus est bien un arbre binaire de recherche.

À faire vous-même 8

Appliquez l'algorithme de parcours infixe sur l'arbre ci-dessous :

Que remarquez-vous ?

Recherche d'une clé dans un arbre binaire de recherche

Nous allons maintenant étudier un algorithme permettant de rechercher une clé de valeur k dans un arbre binaire de recherche. Si k est bien présent dans l'arbre binaire de recherche, l'algorithme renvoie vrai, dans le cas contraire, il renvoie faux.

À faire vous-même 9

Étudiez l'algorithme suivant:


VARIABLE
T : arbre
x : noeud
k : entier
DEBUT
ARBRE-RECHERCHE(T,k) :
  si T == NIL :
    renvoyer faux
  fin si
  x ← T.racine
  si k == x.clé :
    renvoyer vrai
  fin si
  si k < x.clé :
    renvoyer ARBRE-RECHERCHE(x.gauche,k)
  sinon :
    renvoyer ARBRE-RECHERCHE(x.droit,k)
  fin si
FIN

À faire vous-même 10

Appliquez l'algorithme de recherche d'une clé dans un arbre binaire de recherche sur l'arbre ci-dessous. On prendra k = 13.

À faire vous-même 11

Appliquez l'algorithme de recherche d'une clé dans un arbre binaire de recherche sur l'arbre ci-dessous. On prendra k = 16.

Cet algorithme de recherche d'une clé dans un arbre binaire de recherche ressemble beaucoup à la recherche dichotomique vue en première dans le cas où l'arbre binaire de recherche traité est équilibré. La complexité en temps dans le pire des cas de l'algorithme de recherche d'une clé dans un arbre binaire de recherche équilibré est donc $O(log_2(n))$. Dans le cas où l'arbre est filiforme, la complexité est $O(n)$. Rappelons qu'un algorithme en $O(log_2(n))$ est plus "efficace" qu'un algorithme en $O(n)$.

À noter qu'il existe une version dite "itérative" (qui n'est pas récursive) de cet algorithme de recherche :

À faire vous-même 12

Étudiez l'algorithme suivant:


VARIABLE
T : arbre
x : noeud
k : entier
DEBUT
ARBRE-RECHERCHE_ITE(T,k) :
  x ← T.racine
  tant que T ≠ NIL et k ≠ x.clé :
    x ← T.racine
    si k < x.clé :
      T ← x.gauche
    sinon :
      T ← x.droit
    fin si
  fin tant que
  si k == x.clé :
    renvoyer vrai
  sinon :
    renvoyer faux
  fin si
FIN

Insertion d'une clé dans un arbre binaire de recherche

Il est tout à fait possible d'insérer un noeud y dans un arbre binaire de recherche (non vide) :

À faire vous-même 13

Étudiez l'algorithme suivant:


VARIABLE
T : arbre
x : noeud
y : noeud
DEBUT
ARBRE-INSERTION(T,y) :
  x ← T.racine
  tant que T ≠ NIL :
    x ← T.racine
    si y.clé < x.clé :
      T ← x.gauche
    sinon :
      T ← x.droit
    fin si
  fin tant que
  si y.clé < x.clé :
    insérer y à gauche de x
  sinon :
    insérer y à droite de x
  fin si
FIN

À faire vous-même 14

Appliquez l'algorithme d'insertion d'un noeud y dans un arbre binaire de recherche sur l'arbre ci-dessous. On prendra y.clé = 16.

FICHE REVISION

Auteur : David Roche