À faire vous-même 1
Soit le graphe suivant :
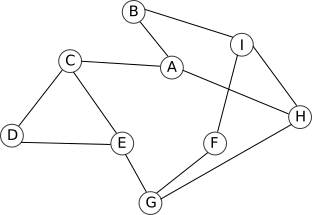
Proposez une implémentation de ce graphe en Python (graphe 1 dans la suite du projet)
À faire vous-même 2
Soit l'algorithme de parcours en largeur d'abord :
VARIABLE
G : un graphe
s : noeud (origine)
u : noeud
v : noeud
f : file (initialement vide)
//On part du principe que pour tout sommet u du graphe G, u.couleur = blanc à l'origine
DEBUT
s.couleur ← noir
enfiler (s,f)
tant que f non vide :
u ← defiler(f)
pour chaque sommet v adjacent au sommet u :
si v.couleur n'est pas noir :
v.couleur ← noir
enfiler(v,f)
fin si
fin pour
fin tant que
FIN
Implémentez cet algorithme en Python. Vous testerez votre programme à l'aide du graphe 1. Il faudra que votre programme fournisse la liste des sommets parcourus en partant du sommet A (il faudra être attentif à l'ordre des sommets dans cette liste)
À faire vous-même 3
Soit l'algorithme de parcours en profondeur d'abord (version non récursive):
VARIABLE
s : noeud (origine)
G : un graphe
u : noeud
v : noeud
p : pile (pile vide au départ)
//On part du principe que pour tout sommet u du graphe G, u.couleur = blanc à l'origine
DEBUT
s.couleur ← noir
piler(s,p)
tant que p n'est pas vide :
u ← depiler(p)
pour chaque sommet v adjacent au sommet u :
si v.couleur n'est pas noir :
v.couleur ← noir
piler(v,p)
fin si
fin pour
fin tant que
FIN
Implémentez cet algorithme en Python. Vous testerez votre programme à l'aide du graphe 1. Il faudra que votre programme fournisse la liste des sommets parcourus en partant du sommet A (il faudra être attentif à l'ordre des sommets dans cette liste)
À faire vous-même 4
Soit l'algorithme de parcours en profondeur d'abord (version récursive):
VARIABLE
G : un graphe
u : noeud
v : noeud
//On part du principe que pour tout sommet u du graphe G, u.couleur = blanc à l'origine
DEBUT
PARCOURS-PROFONDEUR(G,u) :
u.couleur ← noir
pour chaque sommet v adjacent au sommet u :
si v.couleur n'est pas noir :
PARCOURS-PROFONDEUR(G,v)
fin si
fin pour
FIN
Implémentez cet algorithme en Python. Vous testerez votre programme à l'aide du graphe 1. Il faudra que votre programme fournisse la liste des sommets parcourus en partant du sommet A (il faudra être attentif à l'ordre des sommets dans cette liste)
À faire vous-même 5
Soit l'algorithme de détection des cycles :
VARIABLE
s : noeud (noeud quelconque)
G : un graphe
u : noeud
v : noeud
p : pile (vide au départ)
//On part du principe que pour tout sommet u du graphe G, u.couleur = blanc à l'origine
DEBUT
CYCLE():
piler(s,p)
tant que p n'est pas vide :
u ← depiler(p)
pour chaque sommet v adjacent au sommet u :
si v.couleur n'est pas noir :
piler(v,p)
fin si
fin pour
si u est noir :
renvoie Vrai
sinon :
u.couleur ← noir
fin si
fin tant que
renvoie Faux
FIN
Implémentez cet algorithme en Python. Vous testerez votre programme à l'aide du graphe 1 et sur le graphe 2 (voir ci-dessous). Il faudra que votre fonction renvoie "vrai" si un cycle est présent et "faux" dans le cas contraire
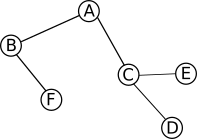
À faire vous-même 6
Soit l'algorithme de recherche de chaine entre 2 sommets :
VARIABLE
G : un graphe
start : noeud (noeud de départ)
end : noeud (noeud d'arrivé)
u : noeud
chaine : ensemble de noeuds (initialement vide)
DEBUT
TROUVE-CHAINE(G, start, end, chaine):
chaine = chaine ⋃ start //le symbol ⋃ signifie union, il permet d'ajouter le noeud start à l'ensemble chaine
si start est identique à end :
renvoie chaine
fin si
pour chaque sommet u adjacent au sommet start :
si u n'appartient pas à chaine :
nchemin = TROUVE-CHAINE(G, u, end, chaine)
si nchemin non vide :
renvoie nchemin
fin si
fin si
fin pour
renvoie NIL
FIN
Implémentez cet algorithme en Python. Vous testerez votre programme à l'aide du graphe 1 (sommet de départ A, sommet d'arrivée G). Il faudra que votre programme fournisse la liste des sommets qui constituent la chaine.

Auteur : David Roche