Algorithmique
Propriétaire des ressources ci-dessous : ministère de l'Éducation nationale et de la jeunesse, licence CC BY SA NC
Voici une sélection de questions issues de la banque nationale de sujets, répondez à ces questions (attention, cette sélection n'est pas exhaustive).
Vous trouverez les corrections à télécharger ici (format tableur OpenDocument)
Q1 - Pour pouvoir utiliser un algorithme de recherche par dichotomie dans une liste, quelle précondition doit être vraie ?
Réponses :
A- la liste doit être triée
B- la liste ne doit pas comporter de doublons
C- la liste doit comporter uniquement des entiers positifs
D- la liste doit être de longueur inférieure à 1024
Q2 - On exécute le script suivant :
for i in range(n):
for j in range(i):
print('NSI')
Combien de fois le mot NSI est-il affiché ?
Réponses :
A- n2
B- (n+1)2
C- 1+2+....+(n-1)
D- 1+2+....+(n-1)+n
Q3 - On considère la fonction suivante :
def trouverLettre(phrase,lettre):
indexResultat = 0
for i in range(len(phrase)):
if phrase[i]== lettre:
indexResultat=i
return indexResultat
Que renvoie l'appel trouverLettre("Vive l’informatique","e") ?
Réponses :
A- 3
B- 4
C- 18
D- "e"
Q4 - Quel code parmi les quatre proposés ci-dessous s'exécute-t-il en un temps linéaire en n (c'est-à-dire avec un temps d'exécution majoré par A x n + B où A et B sont deux constantes) ?
Réponses :
A-
for i in range(n//2):
for j in range(i+1,n):
print('hello')
B-
for i in range(n):
print('hello')
C-
L = [ i+j for i in range(n) for j in range(n) ]
for x in L:
print('hello')
D-
for i in range(n//2):
for j in range(n//2):
print('hello')
Q5 - Combien d’échanges effectue la fonction Python suivante pour trier un tableau de 10 éléments au pire des cas ?
def tri (tab):
for i in range (1, len(tab)):
for j in range (len(tab) - i):
if tab[j]>tab[j+1]:
tab[j],tab[j+1] = tab[j+1], tab[j]
Réponses :
A- 10
B- 45
C- 55
D- 100
Q6 - Pour rendre la monnaie, il est possible d'utiliser un algorithme glouton.
Une seule des affirmations suivantes est vraie :
Réponses :
A- Avec un algorithme glouton, on rend la monnaie en commençant toujours par la pièce ayant la plus grande valeur possible et en procédant ensuite par valeurs décroissantes.
B- Avec un algorithme glouton, on rend la monnaie en commençant toujours par la pièce de plus petite valeur afin de maximiser le nombre de pièces rendues.
C- Quel que soit le type de pièces dans un pays donné, un algorithme glouton donne toujours la monnaie de manière optimale.
D- Un algorithme glouton procède en testant toutes les combinaisons possibles de pièces afin de trouver le rendu optimal.
Q7 - La fonction suivante doit calculer le produit de tous les éléments de la liste passée en paramètre. Avec quelles expressions doit-on la compléter pour que cette fonction soit correcte ?
def produit (L):
p = ...
for elt in L:
.......
return p
Réponses :
A- 1 puis p = p * elt
B- 0 puis p = p * elt
C- 1 puis p = elt
D- 0 puis p = elt
Q8 - La fonction suivante prend en paramètre un tableau non vide de nombres réels.
def mystere(T):
k = len(T)
val = T[k-1]
if k == 1:
return T[k-1]
else:
while k >= 0:
if val < T[k-2]:
val = T[k-2]
k = k-1
return val
Quelle est la valeur renvoyée par cette fonction ?
Réponses :
A- la plus grande des valeurs du tableau T
B- la plus petite des valeurs du tableau T
C- la moyenne des valeurs du tableau T
D- la valeur la plus fréquente du tableau T
Q9 - On considère la fonction suivante :
def f(T,i):
indice = i
m = T[i]
for k in range(i+1, len(T)):
if T[k] < m:
indice = k
m = T[k]
return indice
Quelle est la valeur de f([ 7, 3, 1, 8, 19, 9, 3, 5 ], 0) ?
Réponses :
A- 1
B- 2
C- 3
D- 4
Q10 - On exécute le script suivant :
liste = [4,8,12,6,2]
def permute(L):
for k in range(len(L)-1:
if L[k] > L[k+1]:
L[k],L[k+1] = L[k+1],L[k]
permute(liste)
Quelle est la valeur de liste à la fin de l'exécution du script ?
Réponses :
A- [2, 4, 8, 6, 12]
B- [2, 4, 6, 8, 12]
C- [4, 8, 6, 2, 12]
D- [12, 8, 6, 4, 2]
Q11 - Un algorithme de calcul de moyenne est implémenté de la façon suivante :
def moyenne(liste) :
t = 0
for e in liste :
t = t + e
# assertion vraie à cet endroit
return t/len(liste)
Parmi les propositions suivantes, laquelle reste vraie à la fin de chaque itération de la boucle ?
Réponses :
A- e vaut le nombre de passages dans la boucle
B- t vaut la somme des éléments visités de la liste
C- t vaut la moyenne des éléments visités de la liste
D- après k passages dans la boucle la liste contient k termes
Q12 - Quel est le coût d'un algorithme de recherche du maximum d'un tableau de nombres ?
Réponses :
A- constant
B- logarithmique
C- linéaire
D- quadratique
Q13 - Que calcule la fonction suivante ?
def mystere(liste):
valeur_de_retour = True
indice = 0
while indice < len(liste) - 1:
if liste[indice] > liste[indice + 1]:
valeur_de_retour = False
indice = indice + 1
return valeur_de_retour
Réponses :
A- la valeur du plus grand élément de la liste passée en paramètre
B- la valeur du plus petit élément de la liste passée en paramètre
C- une valeur booléenne indiquant si la liste passée en paramètre est triée
D- une valeur booléenne indiquant si la liste passée en paramètre contient plusieurs fois le même élément
Q14 - La recherche dichotomique est un algorithme rapide qui permet de trouver ou non la présence d’un élément dans un tableau. Mais, pour l’utiliser, une contrainte est indispensable, laquelle ?
Réponses :
A- le tableau ne contient que des nombres positifs
B- la longueur du tableau est une puissance de 2
C- le tableau est trié en ordre croissant
D- le tableau ne contient pas la valeur 0
Q15 - On considère le code suivant de recherche d'une valeur dans une liste :
def search(x, y):
# x est la valeur à chercher
# y est une liste de valeurs
for i in range(len(y)):
if x == y[i]:
return i
return None
Quel est le coût de cet algorithme ?
Réponses :
A- constant
B- logarithmique
C- linéaire
D- quadratique
Q16 - On exécute le script suivant :
liste = [17, 12, 5, 18, 2, 7, 9, 15, 14, 20]
somme = 0
i = 0
while i < len(liste):
somme = somme + liste[i]
i = i + 1
resultat = somme / len(liste)
Quelle affirmation est fausse parmi les suivantes ?
Réponses :
A- le corps de la boucle a été exécuté 10 fois
B- à la fin de l'exécution la valeur de i est 9
C- resultat contient la moyenne des éléments de liste
D- len est une fonction
Q17 - La fonction mystere suivante prend en argument un tableau d'entiers.
def mystere(t):
for i in range(len(t) - 1):
if t[i] + 1 != t[i+1]:
return False
return True
À quelle condition la valeur renvoyée par la fonction est-elle True ?
Réponses :
A- si le tableau passé en argument est une suite d'entiers consécutifs
B- si le tableau passé en argument est trié en ordre croissant
C- si le tableau passé en argument est trié en ordre décroissant
D- si le tableau passé en argument contient des entiers tous identiques
Q18 - Soit l'algorithme suivant, qui permet de retrouver l'index de l'élément maximum dans un tableau de données :
def maximum(T) :
index= 0
for i in range(len(T)) :
if ...... :
index = i
return index
Compléter l'instruction conditionnelle pour que la fonction calcule le résultat attendu :
Réponses :
A- i > index
B- T[i] < T[index]
C- T[i] > T[index]
D- T[index] > T[i]
Q19 - Que renvoie la fonction suivante quand on l'appelle avec un nombre entier et une liste d'entiers ?
def mystere(n,L):
for x in L:
if n == x:
return True
return False
Réponses :
A- une valeur booléenne indiquant si le nombre n est présent au moins une fois dans la liste L
B- une valeur booléenne indiquant si le nombre n est présent plusieurs fois dans la liste L
C- une valeur booléenne indiquant si le nombre n est le plus grand de la liste L
D- une valeur booléenne indiquant si le nombre n est le plus petit de la liste L
Q20 - Quel est l’ordre de grandeur du coût du tri par insertion (dans le pire des cas) ?
Réponses :
A- l'ordre de grandeur du coût dépend de l'ordinateur utilisé
B- linéaire en la taille du tableau à trier
C- quadratique en la taille du tableau à trier
D- indépendant de la taille du tableau à trier
Q21 - En utilisant une recherche dichotomique, combien faut-il de comparaisons avec l'opérateur == pour trouver une valeur dans un tableau trié de 1000 nombres, dans le pire cas ?
Réponses :
A- 3
B- 10
C- 1000
D- 1024
Q22 - On considère le code incomplet suivant qui recherche le maximum dans une liste.
liste = [5,12,15,3,15,17,29,1]
iMax = 0
for i in range(1,len(liste)):
............
iMax = i
print (liste[iMax])
Par quoi faut-il remplacer la ligne pointillée ?
Réponses :
A- if i > iMax:
B- if liste[i] > liste[iMax]:
C- if liste[i] > iMax:
D- if i > liste[iMax]:
Q23 - À la fin de l'exécution du code suivant, quelle sera la valeur de la variable cpt ?
a = 1
cpt = 20
while cpt > 8:
a = 2*a
cpt = cpt - 1
Réponses :
A- 0
B- 7
C- 8
D- 9
Q24 - On considère le code suivant, où n désigne un entier au moins égal à 2.
p = 1
while p < n:
p = 2*p
Quel argument permet d'affirmer que son exécution termine à coup sûr ?
Réponses :
A- p est une puissance de 2
B- toute boucle while termine
C- les valeurs successives de p constituent une suite d'entiers positifs strictement croissante
D- les valeurs successives de n – p constituent une suite d'entiers positifs strictement décroissante
Q25 - On définit la fonction suivante :
def traitement(liste) :
m = liste[0]
for i in range (len(liste)) :
if liste[i] > m:
m = liste[i]
return m
Que vaut traitement([-2,5,6,-10,35]) ?
Réponses :
A- None
B- -10
C- -6
D- 35
Q26 - Un algorithme de recherche dichotomique dans une liste triée de taille n nécessite, dans le pire des cas, exactement k comparaisons.
Combien cet algorithme va-t-il utiliser, dans le pire des cas, de comparaisons sur une liste de taille 2n ?
Réponses :
A- k
B- k+1
C- 2k
D- 2k+1
Q27 - La fonction ci-dessous renvoie le maximum d'une liste.
def maximum(L):
m = L[0]
for i in range(1,len(L)):
#
if L[i] > m:
m = L[i]
return m
Au passage dans la ligne marquée d'un #, quelle propriété reste toujours vérifiée ?
Réponses :
A- m est le maximum des éléments L[k] pour i <= k < len(L)
B- m est le maximum des éléments L[k] pour i < k < len(L)
C- m est le maximum des éléments L[k] pour 0 <= k < i
D- m est le maximum des éléments L[k] pour 0 <= k <= i
Q28 - On considère la fonction suivante :
def comptage(phrase,lettre):
i = 0
for j in phrase:
if j == lettre:
i = i+1
return i
Que renvoie l'appel comptage("Vive l’informatique","e") ?
Réponses :
A- 0
B- 2
C- 19
D- 'e'
Q29 - On considère la fonction suivante :
def f(x,L):
i = 0
j = len(L)-1
while i<j:
k = (i+j)//2
if x <= L[k]:
j = k
else:
i = k + 1
return i
Cette fonction implémente :
Réponses :
A- le tri par insertion
B- le tri par sélection
C- la recherche dichotomique
D- la recherche du plus proche voisin
Q30 - On suppose qu'au début de l'exécution la variable K contient un entier positif non nul.
Lequel des scripts suivants va boucler indéfiniment ?
Réponses :
A-
i = K+1
while i < K:
i = i + 1
B-
i = K-1
while i < K:
i = i - 1
C-
i = K-1
while i < K:
i = i + 1
D-
i = K+1
while i >= K:
i = i - 1
Q31 - Au cours d’un tri de tableau, on observe les étapes suivantes :
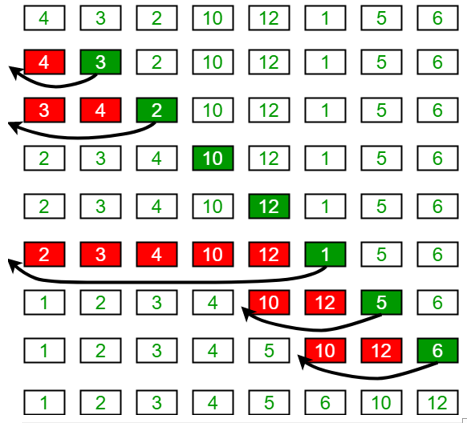
Quel est l’algorithme de tri qui a été utilisé ?
Réponses :
A- tri par sélection
B- tri à bulles
C- tri par insertion
D- tri rapide
Q32 -
def traitement(tableau):
r = 0
for i in range(1, len(tableau)):
if tableau[i] > tableau[r]:
r = i
return r
Cette fonction dont le paramètre est un tableau de nombres renvoie :
Réponses :
A- la somme des éléments du tableau passé en paramètre
B- la moyenne des éléments du tableau passé en paramètre
C- l'élément le plus grand du tableau passé en paramètre
D- l'indice (ou index) du plus grand élément du tableau passé en paramètre
Q33 - Quelle est la valeur du couple (s,i) à la fin de l'exécution du script suivant ?
s = 0
i = 1
while i < 5:
s = s + i
i = i + 1
Réponses :
A- (4, 5)
B- (10, 4)
C- (10, 5)
D- (15, 5)
Q34 - On dispose en quantité illimité de pièces de 1 euro, 2 euros et 5 euros. On veut totaliser une somme de 18 euros. Quelle est la solution donnée par l’algorithme glouton ?
Réponses :
A- [5, 5, 5, 2, 1]
B- [5, 5, 5, 2, 2, 1]
C- [5, 5, 2, 2, 2, 1, 1]
D- [5, 2, 2, 2, 2, 1, 1, 1, 1, 1]
Q35 - Un algorithme de tri d’une liste d’entiers est implémenté de la façon suivante :
def trier(L) :
for i in range(len(L)):
indice_min = i
for j in range(i+1, len(L)):
if L[j] < L[indice_min] :
indice_min = j
L[i], L[indice_min] = L[indice_min], L[i]
return L
Quelle est l'affirmation exacte ?
Réponses :
A- cet algorithme est celui du tri par sélection et il a un coût linéaire en la taille de la liste à trier
B- cet algorithme est celui du tri par insertion et il a un coût linéaire en la taille de la liste à trier
C- cet algorithme est celui du tri par sélection et il a un coût quadratique en la taille de la liste à trier
D- cet algorithme est celui du tri par insertion et il a un coût quadratique en la taille de la liste à trier
Q36 - Soit T le temps nécessaire pour trier, à l'aide de l'algorithme du tri par insertion, une liste de 1000 nombres entiers. Quel est l'ordre de grandeur du temps nécessaire, avec le même algorithme, pour trier une liste de 10 000 entiers, c'est-à-dire une liste dix fois plus grande ?
Réponses :
A- à peu près le même temps T
B- environ 10 x T
C- environ 100 x T
D- environ T2
Q37 - À quelle catégorie appartient l’algorithme des k plus proches voisins ?
Réponses :
A- algorithmes de tri
B- algorithmes gloutons
C- algorithmes de recherche de chemins
D- algorithmes de classification et d’apprentissage
Q38 - Quelle est la valeur de c à la fin de l'exécution du code suivant :
L = [1,2,3,4,1,2,3,4,0,2]
c = 0
for k in L:
if k == L[1]:
c = c+1
Réponses :
A- 0
B- 2
C- 3
D- 10
Q39 - On exécute le code suivant :
tab = [1, 4, 3, 8, 2]
S = 0
for i in range(len(tab)):
S = S + tab[i]
Que vaut la variable S à la fin de l'exécution ?
Réponses :
A- 1
B- 8
C- 18
D- 3.6
Q40 - La fonction maximum doit renvoyer la valeur maximale d'un tableau de nombres. Par quoi doit-on remplacer les pointillés pour qu'elle donne le résultat attendu ?
def maximum(T):
maxi = T[0]
for i in range(len(T)):
.... T[i] > maxi:
......
return maxi
Réponses :
A- if puis, sur la ligne suivante, maxi = T[i]
B- while puis, sur la ligne suivante, maxi = T[i]
C- if puis, sur la ligne suivante, maxi = maxi + 1
D- while puis, sur la ligne suivante, maxi = maxi + 1
Q41 - On dispose de sacs de jetons portant les nombres 10, 5, 3 et 1.
On veut obtenir un total de 21 en utilisant ces jetons.
Si on utilise le principe de l'algorithme glouton, quelle addition va-t-on réaliser pour obtenir ce total de 21 ?
Réponses :
A- 5 + 5 + 5 + 5 + 1
B- 10 + 5 + 3 + 3
C- 10 + 5 + 5 + 1
D- 10 + 10 + 1
Q42 - On a représenté sur un quadrillage les éléments de quatre classes (chaque classe est représentée par un carré, un triangle, un losange ou un disque) ainsi qu’un nouvel élément X.
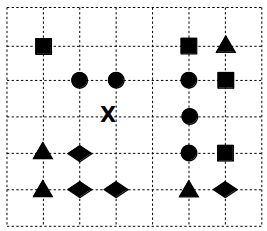
En appliquant l'algorithme des k plus proches voisins pour la distance usuelle dans le plan, avec k=5, à quelle classe est affecté le nouvel élément X ?
Réponses :
A- la classe des carrés
B- la classe des triangles
C- la classe des losanges
D- la classe des disques
Q43 - À quelle catégorie appartient l’algorithme classique de rendu de monnaie ?
Réponses :
A- les algorithmes de classification et d'apprentissage
B- les algorithmes de tri
C- les algorithmes gloutons
D- les algorithmes de mariages stables
Q44 - Qu'affiche le programme suivant :
a = 3
b = 4
if a > b and a == 3:
print('vert')
if a > b and b == 4:
print('rouge')
if a == 4 or b > a:
print('bleu')
if a == 3 or a < b:
print('jaune')
Réponses :
A- vert
rouge
B- bleu
jaune
C- bleu
D- vert
jaune
Q45 - Quelle est la valeur de X/m à la fin de l'exécution du code suivant :
L = [1,2,3,4,1,2,3,4,0,2]
X = 0
m = 0
for k in L:
X = X + k
m = m + 1
Réponses :
A- 2
B- 2.2
C- 10
D- 22
Q46 - Soit L une liste de n nombres réels (n entier naturel non nul). On considère l'algorithme suivant, en langage Python, calculant la moyenne des éléments de L.
M = 0
for k in range(n):
M = M + L[k]
M = M/n
Si le nombre n de données double alors le temps d'exécution de ce script :
Réponses :
A- reste le même
B- double aussi
C- est multiplié par n
D- est multiplié par 4
Q47 - Quel est le coût d'un algorithme de tri par insertion ?
Réponses :
A- constant
B- logarithmique
C- linéaire
D- quadratique
Q48 - Quelle est la complexité du tri par sélection ?
Réponses :
A- inconnue
B- linéaire
C- quadratique
D- exponentielle
Q49 - La fonction ci-dessous compte le nombre d'occurrences d'un élément x dans une liste L :
def compteur(L,x):
n = 0
for item in L:
if item == x:
n = n + 1
return n
Comment évolue le temps d'exécution d'un appel de cette fonction si on prend comme argument une liste deux fois plus grande ?
Réponses :
A- c'est le même temps d'exécution
B- le temps d'exécution est à peu près doublé
C- le temps d'exécution est à peu près quadruplé
D- impossible de le prévoir, cela dépend aussi de l'argument x
Q50 - On exécute le script suivant :
def f(L,x):
r = 0
for e in L:
if e >= x:
r = r + 1
return r
Quelle est la valeur renvoyée par l'appel f([1,2,2,8,3,5,6,0,10],5) ?
Réponses :
A- 2
B- 3
C- 4
D- 5
Q51 - a et m étant deux entiers supérieurs à 1, la fonction suivante renvoie an .
def puissance(a,m):
p = 1
n = m
q = a
while n > 0:
if n%2 == 0:
q = q * q
#
n = n // 2
else:
p = q * p
n = n - 1
return p
Quelle est l'égalité qui est vérifiée à chaque passage par la ligne marquée # ?
Réponses :
A- p x qn-1 = am
B- p x q2n = am
C- p x qn = am
D- p x qn/2 = am
Q52 - Pour trier par sélection une liste de 2500 entiers, le nombre de comparaisons nécessaires à l’algorithme est de l’ordre de :
Réponses :
A- √2500
B- 2500
C- 25002
D- 22500
Q53 - L'algorithme suivant permet de calculer la somme des N premiers entiers, où N est un nombre entier donné :
i =0
somme =0
while i < N :
i = i +1
somme = somme + i
Un invariant de boucle de cet algorithme est le suivant :
Réponses :
A- somme = 0 + 1 + 2 + ... + i et i < N
B- somme = 0 + 1 + 2 + ... + N et i < N
C- somme = 0 + 1 + 2 + ... + i et i < N+1
D- somme = 0 + 1 + 2 + ... + N et i < N+1
Q54 - Un algorithme de tri d’une liste d’entiers est implémenté de la façon suivante :
def trier(L) :
for i in range(len(L)):
indice_min = i
for j in range(i+1, len(L)):
if L[j] < L[indice_min] :
indice_min = j
L[i], L[indice_min] = L[indice_min], L[i]
# assertion vraie à cet endroit
return L
Parmi les assertions suivantes laquelle reste vraie à chaque itération de la boucle, à l'endroit indiqué ci-dessus ?
Réponses :
A- la sous-liste L[0:i+1] contient les i plus grandes valeurs de L triées par ordre décroissant
B- la sous-liste L[0:i+1] contient les i plus grandes valeurs de L triées par ordre croissant
C- la sous-liste L[0:i+1] contient les i plus petites valeurs de L triées par ordre décroissant
D- la sous-liste L[0:i+1] contient les i plus petites valeurs de L triées par ordre croissant
Q55 - On exécute le script suivant :
compt = 0
resultat = 1
while compt !=7 :
resultat = resultat * compt
compt = compt + 1
Laquelle de ces affirmations est vraie ?
Réponses :
A- Le script ne s'arrête pas
B- Le script entre 7 fois dans la boucle et à la fin de son exécution, resultat vaut 0
C- Le script entre 7 fois dans la boucle et à la fin de son exécution, resultat vaut 720
D- Le script entre 6 fois dans la boucle et à la fin de son exécution, resultat vaut 0
Q56 - Quelle est la valeur de element à la fin de l'exécution du code suivant :
L = [1,2,3,4,1,2,3,4,0,2]
element = L[0]
for k in L:
if k > element:
element = k
Réponses :
A- 0
B- 1
C- 4
D- 10
Q57 - Un algorithme est dit glouton si :
Réponses :
A- Il consomme énormément de mémoire
B- Il contient de nombreuses lignes de code
C- Il s’inspire de la méthode de John Elwood Glouton
D- Il fait à chaque étape le choix localement optimum
Q58 - Quelle valeur permet de compléter l’affirmation suivante : « Le nombre d’opérations nécessaires pour rechercher un élément séquentiellement dans un tableau de longueur n est de l’ordre de … » ?
Réponses :
A- 1
B- n
C- n2
D- n3
Q59 - Une seule des affirmations suivantes est vraie :
Réponses :
A- L'algorithme des k plus proches voisins a pour but de déterminer les k plus proches voisins d'une observation dans un ensemble de données.
B- L'algorithme des k plus proches voisins a pour but de déterminer la classe d'une observation à partir des classes de ses k plus proches voisins.
C- L'algorithme des k plus proches voisins a pour but de déterminer dans un ensemble de données le sous-ensemble à k éléments qui sont les plus proches les uns des autres.
D- L'algorithme des k plus proches voisins a pour but de déterminer les éléments d'un ensemble de données appartenant à une même classe.
Q60 - On décide d'effectuer une recherche dans un tableau trié contenant 42000 valeurs. On procède par dichotomie. Le nombre maximal d'itérations de l'algorithme sera :
Réponses :
A- 21000 car une recherche dichotomique divise le nombre de tests maximal par deux.
B- 42000 car la valeur recherchée pourrait très bien être la dernière du tableau.
C- 41999 car si on n'a pas trouvé l'élément recherché à l'avant-dernière position du tableau, il n'est plus utile d'effectuer de test pour la dernière position.
D- 16 car à chaque itération, le nombre d'éléments à examiner est divisé par deux et que 215 <= 42000 <= 216
Q61 - On définit la fonction f comme suit :
def f(L):
a = L[0]
for x in L:
if x < a:
a = x
return a
Quelle est la valeur renvoyée par l'appel f([7, 10.3, -4, 12 ,7 ,2, 0.7, -5, 14, 1.4]) ?
Réponses :
A- -5
B- 1.4
C- 7
D- 14
Q62 - La fonction suivante doit déterminer la valeur maximale d'un tableau de nombres passé en argument. Avec quelles expressions faut-il remplacer les pointillés du script suivant pour que la fonction soit correcte ?
def maximum(T):
maxi = T[0]
n = len(T)
for i in range(i, .....):
if T[i] > maxi:
maxi = ......
return maxi
Réponses :
A- n puis T[i]
B- n puis T[i-1]
C- n-1 puis T[i]
D- n-1 puis T[i-1]
Q63 - La fonction suivante doit calculer la moyenne d’un tableau de nombres, passé en paramètre. Avec quelles expressions faut-il remplacer les points de suspension pour que la fonction soit correcte ?
def moyenne(tableau):
total = ...
for valeur in tableau:
total = total + valeur
return total / ...
Réponses :
A- 1 et (len(tableau) + 1)
B- 1 et len(tableau)
C- 0 et (len(tableau) + 1)
D- 0 et len(tableau)
Q64 - La fonction ci-dessous permet d’effectuer une recherche par dichotomie de l’index m de l’élément x dans un tableau L de valeurs distinctes et triées.
def dicho(x,L):
g = 0
d = len(L)-1
while g <= d:
m = (g+d)//2
if L[m] == x:
return m
elif L[m] < x:
g = m+1
else:
d = m-1
return None
Combien de fois la cinquième ligne du code de la fonction (m = (g+d)//2) sera-t-elle exécutée dans l'appel dicho(32, [4, 5, 7, 25, 32, 50, 51, 60]) ?
Réponses :
A- 1 fois
B- 2 fois
C- 3 fois
D- 4 fois
Q65 - Avec un algorithme de recherche par dichotomie, combien de comparaisons sont-elles nécessaires pour s’assurer que 22 n’est pas dans la liste suivante :
[1, 5, 9, 12, 20, 21, 24, 32, 35, 40, 41, 47, 53, 60, 70]
Réponses :
A- 2
B- 4
C- 7
D- 13
Q66 - On définit une fonction de calcul de la moyenne d'une liste de nombres :
def moyenne(L):
s = 0
n = len(L)
for x in L:
s = s + x
return s/n
Combien cette fonction utilise-t-elle d'additions et de divisions pour calculer la moyenne d'une liste de 7 nombres ?
Réponses :
A- 7
B- 8
C- 9
D- 10
Q67 - Avec un algorithme de recherche par dichotomie, combien d’étapes sont nécessaires pour déterminer que 35 est présent dans le tableau [1, 7, 12, 16, 18, 20, 24, 28, 35, 43, 69] ?
Réponses :
A- 1 étape
B- 2 étapes
C- 9 étapes
D- 11 étapes
Q68 - Que fait la fonction suivante :
def trouver(L):
i = 0
for j in range(1, len(L)):
if L[j] >= L[i]:
i = j
return i
Réponses :
A- elle renvoie le maximum de la liste
B- elle renvoie le minimum de la liste
C- elle renvoie l’indice de la première occurrence du maximum de la liste
D- elle renvoie l’indice de la dernière occurrence du maximum de la liste
Q69 - On considère la fonction Python suivante, qui prend en argument une liste L et renvoie le maximum des éléments de la liste :
def rechercheMaximum(L):
max = L[0]
for i in range(len(L)):
if L[i] > max:
max = L[i]
return max
On note n la taille de la liste.
Quelle est la complexité en nombre d’opérations de l’algorithme ?
Réponses :
A- constante, c’est-à-dire ne dépend pas de n
B- linéaire, c’est-à-dire de l’ordre de n
C- quadratique, c’est-à-dire de l’ordre de n2
D- cubique, c’est-à-dire de l’ordre de n3
Q70 - La fonction suivante prend en arguments deux entiers positifs et renvoie leur produit.
def produit(a,b):
c = 0
i = 0
while i < b:
#
i = i + 1
c = c + a
return c
Quelle propriété reste vraie à chaque passage par la ligne marquée d'un # ?
Réponses :
A- c = a x (i+1)
B- c = a x (i-1)
C- c = a x i
D- c = a x b
Q71 - On définit :
def traite(chaine,a):
nouvelle_chaine = ""
for k in range(len(chaine)):
if chaine[k] != a:
nouvelle_chaine = nouvelle_chaine + chaine[k]
return nouvelle_chaine
Quelle est la valeur renvoyée par l'appel traite("histoire","i") ?
Réponses :
A- "hstore"
B- "ii"
C- "histoire"
D- ""
Q72 - On exécute le script suivant :
liste=[48, 17, 25 , 9, 34, 12, -5, 89, 54, 12, 78, 8, 155, -85]
def recherche(liste):
valeur_1 = liste[0]
valeur_2 = liste[0]
for item in liste:
if item < valeur_1:
valeur_1 = item
elif item > valeur_2:
valeur_2 = item
return(valeur_1, valeur_2)
Que va renvoyer l'appel recherche(liste) ?
Réponses :
A- (-85,155)
B- [-85,155]
C- (155,-85)
D- [155,-85]
Q73 - On définit une fonction de recherche dichotomique de l'indice d'un élément x à l'intérieur d'une liste triée de la façon suivante:
def recherchee(x, liste_triee):
a = 0
b = len(liste_triee)-1
while a < b:
m = (a + b)//2
if liste_triee[m] == x:
return m
elif liste_triee[m] > x:
b = m - 1
else:
........
return a
Par quoi faut-il remplacer la ligne pointillée pour répondre à l'objectif ?
Réponses :
A- a = m + 1
B- a = m - 1
C- a = b
D- a = b - m