Actualite

Des expériences pour mieux appréhender la croissance exponentielle

Albert Bartlett (1923-2013), professeur de physique à l’Université du Colorado, et qui a donné à partir des années 70 plus de 17209 conférences sur le thème: « arithmétique, population et énergie », ne cessait de répéter:

L’équation du nénuphar

Imaginons un nénuphar planté dans un grand lac qui aurait la propriété héréditaire de produire, chaque jour, un autre nénuphar. Au bout de trente jours, la totalité du lac est couverte et l’espèce meurt étouffée, privée d’espace et de nourriture.
Au bout de combien de jours les nénuphars vont-ils couvrir la moitié du lac ?
Non pas 15 jours, comme on pourrait le penser un peu hâtivement, mais bien 29 jours, c’est-à-dire la veille, puisque le double est obtenu chaque jour.
Si nous étions l’un de ces nénuphars, à quel moment aurions-nous conscience que l’on s’apprête à manquer d’espace ? Au bout du 24ème jour, 97% de la surface du lac est encore disponible et nous n’imaginons probablement pas la catastrophe qui se prépare et pourtant nous sommes à moins d’une semaine de l’extinction de l’espèce…
Et si un nénuphar particulièrement vigilant commençait à s’inquiéter le 27ème jour et lançait un programme de recherche de nouveaux espaces, et que le 29ème jour, trois nouveaux lacs étaient découverts, quadruplant ainsi l’espace disponible ?
Et bien, l’espèce disparaîtrait au bout du … 32ème jour !

Il s’agit d’un texte d’Albert Jacquard (1925-2013), biologiste, généticiens et essayiste français, dans L’Equation du nénuphar : les plaisirs de la science, Calmann-Lévy, 1998.

Ce type de croissance est très facile à expérimenter, même pour les plus jeunes, avec par exemple, un jeu d’échec pour représenter le lac et des pions pour représenter les nénuphars. La case représente l’espace nécessaire au développement d’un nénuphar, si bien que 64 nénuphars peuvent tenir dans ce drôle de lac.
Au bout de combien de jours la totalité du lac est-elle recouverte?
Au bout du 7ème jour! Le premier jour, il y a un nénuphar, le deuxième, 2, .. chaque jour on multiplie le nombre obtenu la veille par 2. La totalité du lac est recouverte lorsque 1 x 2 x 2 x 2 x 2 x 2 x 2 = 64.

Une autre façon de se représenter la croissance des nénuphars, c’est avec un jeu de type kapla: on pose une planchette au sol, puis une autre à côté, puis deux à plat l’une sur l’autre puis quatre… chaque nouvelle colonne est constitué du nombre de planchette déjà au sol, elle mesure les naissances du jour. C’est exactement le principe des diagrammes en bâton. On voit que les colonnes grandissent bien vite et bientôt le stock de planchettes est épuisé: nous n’avons pas pu terminer le cinquième jour avec notre jeu!
Combien faudrait-il de planchettes pour représenter le développement des nénuphars sur 30 jours? Et de combien de planchettes disposez-vous?
Au bout de 30 jours, il y aura =2²⁹ nénuphars. Il faut donc 536 870 912 planchettes et il y a 200 planchettes dans un baril de kapla!

Une croissance de 5 % par an: qu’est-ce cela signifie ?

On parle d’un taux de croissance de t % par unité de temps (l’unité de temps n’est pas nécessairement une année). Durant la deuxième moitié du siècle dernier, la croissance démographique et la croissance économique mondiale ont connues des taux d’accroissement jamais atteints. Jusqu’en 1815, la population augmente au plus de 4 millions d’habitants par an, une croissance linéaire donc, puisque l’augmentation n’est pas proportionnelle à la population, mais constante. De 1960 à 2011, elle est passé de 3 à 7 milliards, soit un taux d’accroissement de 1,5% par an. La croissance économique, mesurée par le PIB (produit intérieur brut), atteignait pas loin de 5% dans les années 60 . Ça fait beaucoup ou pas?

Une bonne façon de se faire une idée est de calculer le temps de doublement: combien faut-il de temps pour que la quantité concernée par le taux de croissance double ?

Par exemple, pour la croissance des nénuphars ci-dessus, quel est le temps de doublement ?
Chaque jour le nombre de nénuphars double, donc le temps de doublement est de 1 jour.
Quel est le taux de croissance journalier de la population de nénuphars ?
Le taux de croissance, c’est la proportion de la population en pourcentage qu’il faut rajouter chaque jour, et dans notre cas c’est la totalité: 100%! C’est énorme!

Lorsque le taux d’accroissement t ne dépasse pas 10 % (ce qui est le cas en économie et en démographie) une formule très simple permet de calculer le temps de doublement T:

On peut calculer ainsi facilement le temps de doublement pour un taux de croissance donnée: par exemple, pour un taux de 3,5 % par an: T=20 ans.
Il s’agit d’une formule approchée, sauriez-vous donner la formule exacte ?
Soit U₀ la quantité initiale, et U_n la quantité obtenue au bout de n années. On a donc une suite de nombres (U_n) et un taux d’accroissement de t% par an, cela signifie que: U_n+1= U_n + U_n * t /100 = U_n (1+t /100).
On reconnait une suite géométrique de raison q=1+t/100. Le terme général de la suite vaut U_n=U₀ qⁿ.
Le temps de doublement, c’est lorsque U_n=2 U₀, soit en simplifiant par U₀, lorsque (1+t/100)ⁿ=2.
En prenant le logarithme népérien, on obtient n ln(1+t/100)= ln(2), soit n= ln (2)/ln(1+t/100).
Or, ln (2)= 0,693 et lorsque t/100 est petit, ln (1+t/100) ~ t/100, ce qui donne notre formule approchée.

Une croissance économique de 5% par an, cela veut donc dire que la production de ressources double en 12 ans!
Dès les années 70, des scientifiques et des économistes, comme Albert Barlett et les membres du club de Rome, se sont émus des forts taux de croissance démographique et ont alerté sur les limites de la croissance. Les physiciens et les biologistes connaissent bien ces phénomènes régis par la croissance exponentielle, comme l’explosion d’un bâton de dynamite ou la propagation d’un virus. Nous allons y revenir.

Perception et logarithme

Dans les années 1840, un médecin allemand, Ernst Weber , a conduit des expériences pour déterminer le degré de sensibilité de la perception humaine. Il cherchait à déterminer la plus petite différence de poids détectable.

On peut faire nous même l’expérience, avec des lots d’objets, plus ou moins lourds. On pourra s’inspirer de l’expérience de pesée proposée par la fondation La main à la pâte.
Quelle différence de poids êtes-vous capable de détecter? Est-ce que cette différence dépend du poids l’objet (relative) ou non (absolue)? Par exemple, est-ce que c’est 100 grammes quel que soit le poids de l’objet pesé ou bien est-ce que la différence détectée est proportionnelle au poids de l’objet: par exemple, 10g pour 100g, mais 100g pour un kilo, soit 10% du poids.
C’est la deuxième réponse qui est la bonne. La plus petite différence de poids détectable est de l’ordre de 20% du poids de l’objet. On parle parfois de sensibilité baryque. C’est en se basant sur les travaux de Weber que le médecin Gustav Fechner (1801–1887) énonça sa loi selon laquelle « la sensation varie comme le logarithme de l’excitation ».

Il ne s’agit pas seulement de la pesée, mais de tous nos sens. D’ailleurs, l’unité de mesure du niveau sonore, le décibel, contient cette loi dans sa définition. Le niveau sonore est en effet relié à l’intensité sonore, i.e. la puissance transportée par l’onde, par une fonction logarithme. Concrètement, lorsque l’intensité sonore est multipliée par deux, le niveau sonore augmente de 3dB. Si une moto produit 90dB, deux motos ne produirons que 93 dB (voir la video « c’est pas sorcier » sur le bruit à 11’30-16′). C’est exactement ce que fait un logarithme: changer un produit en addition. Notre appareil auditif compresse les niveaux d’énergie dans un spectre confortable, ce qui nous permet d’entendre la personne qui chuchote à notre oreille, mais aussi le bruit de décollage d’un avion … sans détruire notre ouïe. Compresser, c’est le rôle de l’échelle logarithmique. Dans une échelle classique, dite linéaire, les graduations successives correspondent à l’addition d’un nombre constant, par exemple 1: 0,1,2,3,4,5,… Dans une échelle logarithmique, les graduations successives correspondent à la multiplication par un nombre constant, par exemple 10 (ce nombre est appelé la base du logarithme): 1,10,100,1000, 10 000, …. L’échelle logarithmique permet donc de représenter des nombres beaucoup plus grand (voir la vidéo sur la chaine youtube MicMath). On pourra aussi lire le chapitre 2 du livre de Jan Stewart: « 17 équations qui ont changé le monde ».

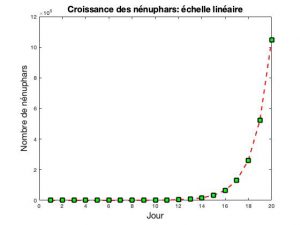
Pour se familiariser avec l’échelle logarithmique, traçons d’abord la croissance de nénuphars sur une représentation graphique: les jours en abscisse et le nombre total de nénuphars en ordonné. On obtient une courbe exponentielle. Sur l’axe des y, les graduations sont espacées de 2x 10⁵ =200 000. Ce qui explique que la courbe soit très plate jusqu’au 12ème jour.
Puis appliquons à l’axe des y une échelle logarithmique en base 2, dans laquelle pour passer d’une graduation à la suivante, on multiplie par 2.

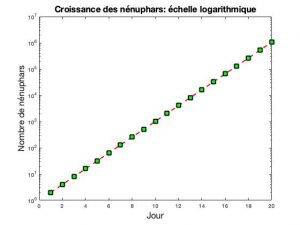Quelle courbe obtient-on? Une droite bien sur !

Ça illustre le fait que logarithme et exponentielle sont des fonctions inverse l’une de l’autre.
Et si on utilise un logarithme en base 10 (ou pour passer d’une graduation à la suivante, on multiplie par 10)? Pouvez-vous le démontrer?
C’est la même chose car y(n)=log₁₀(2ⁿ)= n log₁₀(2). Seule la pente de la droite change. C’est le principe même des logarithmes qui transforment les multiplications en addition!

Les scientifiques, et les médias à leur suite, utilisent systématiquement ce type de représentation pour représenter un phénomène qui croit de manière exponentielle, comme une épidémie. Il est donc très utile de se familiariser avec ce type de représentation afin de les interpréter correctement!

La croissance et ses limites

Aujourd’hui, le taux de la croissance économique n’est plus que l’ordre de 2% et tandis que les voix des scientifiques et de certaines ONG se font de plus en plus fortes pour dénoncer l’impact de la croissance sur le climat et les inégalités sociales, les politiques appellent de leurs vœux le retour d’une croissance forte sans laquelle notre économie ne peut fonctionner… S’il revient à chacun de se faire sa propre idée par rapport à ces prises de positions, comme le soutenait Albert Barlett, les mathématiques peuvent toutefois aider à comprendre les limites de la croissance.

Une belle illustration se trouve dans cette légende :

«  le roi Belkib (Indes, 3 000 ans av. J.C.) promit une récompense fabuleuse à qui lui proposerait une distraction qui le satisferait. Lorsque le sage Sissa, lui présenta le jeu d’échecs, le souverain, demanda à Sissa ce que celui-ci souhaitait en échange de ce cadeau extraordinaire. Sissa demanda au prince de déposer un grain de riz sur la première case, deux sur la deuxième, quatre sur la troisième, et ainsi de suite pour remplir l’échiquier en doublant la quantité de grain à chaque case.  Le prince accorda immédiatement cette récompense sans se douter de ce qui allait suivre. Son conseiller lui expliqua qu’il venait de précipiter le royaume dans la ruine car les récoltes de l’année ne suffiraient pas à payer Sissa. »

Combien faudrait-il mettre de grains de riz sur la dernière case? Au total, combien y aurait-il de grains de riz sur l’échiquier?
Sur la dernière case, il faut mettre 2 x 2 x 2 .. autant de fois qu’il y a de cases sur l’échiquier, sans compter la première, soit 63 fois. Difficile à écrire! Heureusement, les mathématiciens ont adopté une convention pour pouvoir écrire ce chiffre, c’est 2⁶³. Et les ordinateurs nous permettent de calculer ce chiffre 2^63= 9 223 372 036 854 775 808. Pour la quantité totale, il faudra calculer la somme d’une série géométrique de raison 2 et de terme initial 1, on obtient: 2⁶⁴ -1, ce qui fait environ 18 446 744 073 709 551 615 grains soit environ 1,8 10¹⁹. Plus de 18 milliards de milliards de grains !

Supposons que vous ayez un kilo de riz chez vous, combien de cases de l’échiquier pourrez-vous remplir?
Pour le savoir, on peut peser une petite quantité de grains de riz (selon la sensibilité de la balance), puis compter les grains et faire une règle de trois. Certains l’ont fait : Si on prend leur chiffre, 60 000 grains de riz pour un kilo, on voir qu’on remplit 15 cases avec un kilo de riz (on calcule les puissances successives de deux et on s’arrête lorsqu’on a atteint la quantité de grains disponibles).

On se dit qu’on devrait pouvoir y arriver. Qu’en pensez-vous?
Si on fait le calcul, on voit qu’en fait, il faudrait 1,8 10¹⁹/ 60000 ~ 3 10¹⁴ kg de riz. Pour se faire une idée, la production mondiale de riz est de 479 millions de tonnes par an, soit 479 10⁹ kg par an (voir ici ). Elle ne suffirait donc pas! Il faudrait donc plus de 1 000 ans de production mondiale de riz pour atteindre cette faramineuse quantité ! Difficile de satisfaire Sassi !

Pour conclure

Les limites de la croissance sont bien sûr associées aux ressources limitées sur notre planète. Est-ce que les progrès technologiques pourront permettre de résoudre le problème ? Pourra-t-on par exemple coloniser Mars pour sauver l’humanité, comme le propose Elon Musk ? Et pourquoi pas des planètes plus lointaines ?

Ceci soulève la question posée par Fermi (1901-1954) et baptisée paradoxe de Fermi par l’astronome Carl Sagan:
« S’il y avait des civilisations extraterrestres, leurs représentants devraient être déjà chez nous. Où sont-ils donc ? ».

Qu’en pensez-vous ?
Reformulée par Aurélien Crida, astrophysicien à l’UCA (Université Côte d’Azur), cette question s’impose encore plus aujourd’hui: pourquoi, parmi les 50 milliards de planètes terrestres qui ont été découvertes par les astronomes depuis les années 90, n’y en a-t’il pas une qui a 100 ans d’avance sur nous?  Où sont-ils donc! Je vous invite vivement à écouter ce que celui-ci a à nous dire à ce propos !

Ressources

• la vidéo de Albert Barlett modestement intitulée: « the most important video you’ll ever see »
• le livre de Jan Stewart: 17 équations qui ont changé le monde, Flammarion Champs sciences 2015, chapitre 2 sur les logarithmes.
• la vidéo de Mickael Launey (MicMaths): Merveilleux logarithmes
• un article sur échelle linéaire-échelle logarithmique
• les transparents d’Aurélien Crida (c@fe’in à l’Inria Sophia) et une vidéo enregistrée dans le cadre du Climacte 2020 de sa conférence: « Des Exoplanètes au P.I.B.: les limites de la croissance ? »
• un article d’Aurélien Crida: « Exponentielle, Covid-19, et climat »
• un article sur le biais de croissance exponentielle: « Pourquoi notre cerveau ne comprend rien à la propagation du coronavirus. »

PDF view