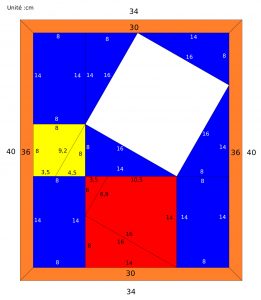
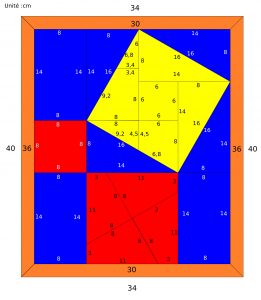
Puzzle de pythagore

I-Présentation

Modèle 1	Modèle 2

Objectif

Ceci démontre le théorème de Pythagore : c² = a² + b²

Le théorème de Pythagore permet de calculer une longueur dans un triangle rectangle, et sa réciproque de savoir si un triangle est rectangle ou non. Le théorème de Pythagore et ses conséquences sont parmi les résultats mathématiques les plus utiles en pratique. Ils sont particulièrement incontournables en architecture, en ingénierie et en robotique.

Histoire

Le théorème de Pythagore doit son nom à Pythagore de Samos, philosophe de la Grèce antique du vi^e siècle av. J.-C.. Cependant le résultat était connu plus de mille ans auparavant en Mésopotamie, et la plus ancienne démonstration qui nous soit parvenue est due à Euclide, vers -300. Même si les mathématiciens grecs en connaissaient sûrement une auparavant, rien ne permet de l’attribuer de façon certaine à Pythagore. Par ailleurs le résultat a vraisemblablement été découvert indépendamment dans plusieurs autres cultures. Les premières démonstrations historiques reposent en général sur des méthodes de calcul d’aire par découpage et déplacement de figures géométriques. Inversement, la conception moderne de la géométrie euclidienne est fondée sur une notion de distance qui est définie pour respecter ce théorème.

Liens

• Quelques puzzles de Pythagore
• Onze puzzles pour le théorème de Pythagore
• Pavage avec un seul type de pièce

II-Construction

Plan de l’objet

•         Modèle 1   

•           Modèle 2

Matériaux

Modèle 1 : 

• 1 planche en bois 34x40cm d’épaisseur 1cm
• 1 planche en bois 14x45cm d’épaisseur 5mm (pour les contours)
• 1 planche en plexi bleu 30x30cm
• 1 planche en plexi rouge 16x25cm
• 1 planche en plexi jaune 20x20cm
• 1 planche en plexi transparente 6x4cm
• 1 colle à bois
• 1 colle à plexi
• 1 imprimante laser ( on en trouve dans les fablab )

Modèle 2 : 

• 1 planche en bois 34x40cm d’épaisseur 1cm
• 1 planche en bois 14x45cm d’épaisseur 5mm (pour les contours)
• 1 planche en plexi bleu 30x30cm
• 1 planche en plexi rouge 16x16cm
• 1 planche en plexi jaune 10x10cm
• 1 planche en plexi transparente 3x4cm
• 1 colle à bois
• 1 colle à plexi
• 1 imprimante laser ( on en trouve dans les FabLab)

Nous avons trouvé tout le matériel dans un de ces magasins de bricolage usuels, le plexi nous a directement été fourni par le FabLab qui disposait du matériel adapté à son imprimante laser. Voici les plans:

Montage

Modèle 1 et 2

• Créer un fichier avec un logiciel vectoriel afin de dessiner les pièces (rouge, jaune et bleu) qui seront en plexi
• Créer un fichier avec un logiciel vectoriel pour dessiner les contours qui seront en bois
• Créer un fichier avec le meme logiciel pour dessiner 5 (modèle 1) ou 12 (modèle 2) carrés 8x8mm qui nous serviront de poignés pour chaque pièce du puzzle (rouge et jaune) qui seront en plexi transparent.
• Imprimer avec l’imprimante laser sur le plexi de couleur correspondante aux pièces , sur la planche en bois pour les contours et sur le plexi transparent pour les poignées.
• Coller sur la planche en bois les contours en bois avec la colle à bois
• Coller les pièces bleu avec de la colle à plexi qui elles sont fixent
• Coller les poignées au milieu de chaque pièce du puzzle (rouge et jaune ) avec la colle à plexi

Ces quelques indications ne vous suivent pas ? Aucun souci : contactez-nous ! Nous serons enchanté·e·s de vous aider à réaliser ces objets.

III-Animation

PDF view