activité 11.1

Le schéma ci-dessous illustre le principe de fonctionnement du tri par insertion pour le tableau [27, 10, 12, 8, 11]

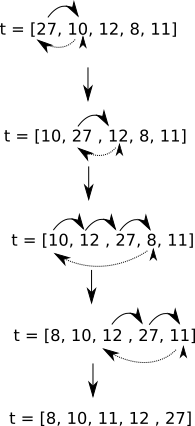
Produisez un schéma équivalent pour le tableau [12, 8, 23, 10, 15]

activité 11.2

Le schéma ci-dessous illustre le principe de fonctionnement du tri par sélection pour le tableau [12, 8, 23, 10, 15]

Produisez un schéma équivalent pour le tableau [15, 16, 11, 13, 12]

activité 11.3

Soit l'algorithme du tri par insertion :

VARIABLE
t : tableau d'entiers
i : nombre entier
j : nombre entier
k : nombre entier
DEBUT
j←2
tant que j<=longueur(t):  
  i←j-1
  k←t[j]
  tant que i>0 et que t[i]>k:
    t[i+1]←t[i]
    i←i-1
  fin tant que
  t[i+1]←k
  j←j+1
fin tant que
FIN

Appliquez cet algorithme au tableau t = [27, 10, 12, 8, 11] et vérifiez que vous obtenez bien le tableau [8, 10, 11, 12, 27]

activité 11.4

Soit l'algorithme du tri par sélection :

VARIABLE
t : tableau d'entiers
i : nombre entier
min : nombre entier
j : nombre entier
DEBUT
i←1
tant que i<longueur(t):  
  j←i+1
  min←i
  tant que j<=longueur(t):  
    si t[j]<t[min]:
      min←j
    fin si
    j←j+1
  fin tant que
  si min≠i :
    échanger t[i] et t[min]
  fin si
  i←i+1
fin tant que
FIN

Appliquez cet algorithme au tableau t = [27, 10, 12, 8, 11] et vérifiez que vous obtenez bien le tableau [8, 10, 11, 12, 27]

activité 11.5

Proposez une implémentation en Python de l'algorithme de tri par insertion. Vous testerez votre programme à l'aide du tableau t = [15, 16, 11, 13, 12]

activité 11.6

Proposez une implémentation en Python de l'algorithme de tri par sélection. Vous testerez votre programme à l'aide du tableau t = [15, 16, 11, 13, 12]