Actualite
2016, 09 Septembre . Bonne feuille . mathématiques . algorithmiqueLa géométrie de la Tortue : des liens entre mathématiques et algorithmique, pour les enseignants
 L’article que publie Yves Martin1 dans MathémaTICE pose la question :
L’article que publie Yves Martin1 dans MathémaTICE pose la question :
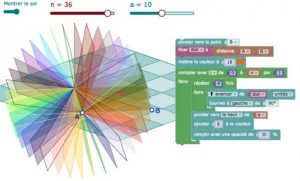
Que devient une tortue plongée dans un champ dynamique ?
En relation avec Eric Hackenhoz, le créateur de DGPad et l’équipe de CaRMetal, Yves Martin développe les possibilités offertes par la Tortue de DGPad et souligne les ruptures didactiques que cela entraîne :
Avec une tortue dynamique, on ne voit pas un hexagone se construire. Plus précisément, il n’y a aucune possibilité de ralentir la tortue pour voir une exécution pas à pas, au contraire tout est donné d’un coup. Mais parce que « tout est donné d’un coup », le paradigme d’usage de la tortue change : l’utilisateur est d’emblée plongé dans une perception globale de ce qu’il est en train de produire. Il n’y a plus cette notion d’exécution, comme si on avait fait sauter une interface intermédiaire (le runtime) entre le codage et sa sortie graphique, avec deux conséquences immédiates à l’utilisation :
• la possibilité d’explorer plus facilement, instantanément, ce que l’on est en train de faire, car tout est paramétrable, et la trace de la tortue est alors modifiée dès que l’on touche à ces paramètres
• et celle de corriger le code en temps réel, comme libéré de l’interfaçage entre l’écriture d’un code et sa mise en oeuvre en sortie graphique.
L’auteur applique ces nouvelles possibilités à de nombreux domaines, en s’interrogeant sur ce que cela apporte à l’enseignement des mathématiques et à la formation des nouveaux enseignants.
Gérard Kunz, SesaMath.
1 Maître de Conférences à l’Université de La Réunion, Formateur d’enseignants à l’ESPE de La Réunion, animateur de l’IREM de La Réunion.
Dernière modification : octobre 2017. Ce contenu est obsolète.