activités chapitre 16

TERMINALE NSI

activité 16.1

Résumez en quelques lignes le principe de la programmation dynamique.

activité 16.2

Cette activité s'inspire librement du contenu du livre de Cormen, Leiserson, Rivest et Stein "Introduction to Algorithms" (édition The Mit Press)

L'entreprise sun & steel produit et vend des barres d'acier de différentes longueurs. Voici le prix de vente de ces barres d'acier en fonction de leurs longueurs :

longueur i en mètre prix p en euro
1 1
2 5
3 8
4 9
5 10
6 17
7 17
8 20
9 24
10 30

Quand l'entreprise produit une barre de longueur n, elle a 2 possibilités :

Par exemple pour une barre de 4 m de longueur l'entreprise peut :

1) Continuez la liste ci-dessus afin d'obtenir toutes les possibilités pour une barre de 4 m. Quel est le revenu maximum possible pour la société ?

Partons maintenant du principe qu'au départ, la barre ne fait plus forcement 4 m mais qu'elle fait n mètres (n compris entre 1 et 10).

Pour chaque longueur n on peut déterminer le revenu maximum possible (que l'on notera rn). Par exemple :

L'idée de cette activité est d'écrire un programme Python qui permettra d'obtenir tous les rn avec n compris entre 1 et 10.

On peut remarquer qu'il est aussi possible de calculer r5 en appliquant la relation suivante :

r5 = max(p5, r1+r4, r2+r3, r3+r2, r4+r1)

avec :

Nous avons donc :

r5 = max(10, 1+5, 5+8, 8+5, 5+1) = max(10,6,13,13,6) = 13

Il est possible de généraliser cette relation en écrivant :

rn = max(pn, r1+rn-1, r2+rn-2,..., rn-1+r1)

2) Retrouvez la valeur de r4 en utilisant la relation ci-dessus

On remarque que pour calculer rn, il faut calculer rn-1, rn-2, ...

Cela devrait vous rappeler quelque chose : dans le chapitre consacré aux fonctions récursives nous avons vu que pour calculer la factorielle de n , il faut calculer la factorielle de n-1, la factorielle de n-2 ... Nous allons donc pouvoir écrire une fonction récursive afin de pouvoir résoudre notre problème (calculer tous les rn pour n compris entre 1 et 10).

Avant d'écrire cette fonction récursive, analysons un peu la relation vue ci-dessus :

rn = max(pn, r1+rn-1, r2+rn-2,..., rn-1+r1)

Dans cette relation, le premier élément (pn) correspond au cas où la barre n'est pas découpée. Les autres éléments correspondent au cas où l'on découpe la barre en 2 morceaux de longueurs i et n-i avec i compris entre 1 et n (avec n inclus).

Il est donc possible de modifier la relation vue ci-dessus et d'écrire :

rn = max(pi+rn-i) avec i compris entre 1 et n (n inclus)

Par exemple, pour n=5, on retrouve :

r5 = max(p1+r4, p2+r3, p3+r2, p4+r1, p5+r0) avec r0 le revenu maximum pour une barre de longueur nulle (on a donc r0 = 0)

Pour calculer r5 il est donc nécessaire de calculer r4 :

r4 = max(p1+r3, p2+r2, p3+r1, p4+r0)

mais il est aussi nécessaire de calculer r3, r2 et r1 à la fois pour calculer r5 mais aussi pour calculer r4 ... On retrouve bien notre structure récursive.

N.B : Si vous avez du mal à comprendre le pourquoi du comment de la relation vue ci-dessus (rn = max(pi+rn-i) avec i compris entre 1 et n (n inclus)), cela n'a pas une grande importance, contentez-vous de l'utiliser (le but de cette activité est ailleurs).

3) La fonction revenu_barre ci-dessous prend en paramètre la taille n de la barre (avant découpe) et renvoie le revenu maximum possible pour cette barre de longueur n :

def revenu_barre(n):
    prix = [0,1,5,8,9,10,17,17,20,24,30]
    if n==0:
        return .........
    r = float('-inf')
    for i in range(1,n+1):
        r = max(r,prix[i]+........)
    return r

Compétez la fonction revenu_barre

4) Utilisez la fonction revenu_barre pour calculer r5, r6, r7, r8, r9 et r10

5) L'entreprise a modifié ces tarifs, nous avons maintenant le tableau suivant :

longueur i en mètre prix p en euro
1 1
2 6
3 9
4 11
5 12
6 19
7 20
8 23
9 24
10 26

Modifiez la fonction revenu_barre afin de tenir compte de cette modification tarifaire.

Comme nous avons eu l'occasion de le voir ci-dessus, pour calculer rn il est nécessaire de calculer rn-1, rn-2...mais pour calculer rn-1, il sera aussi nécessaire de calculer rn-2 ! Nous allons donc calculer 2 fois rn-2.

Afin de mieux visualiser la situation, voici un arbre qui permet de mieux visualiser les calculs nécessaires afin de déterminer r4 :

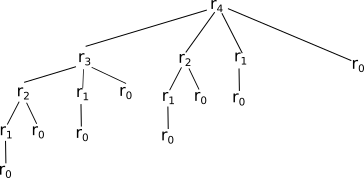
Comme vous pouvez le constater, pour calculer r4, il faut calculer :

Dans cet exemple, cela ne pose aucun problème, mais avec un n plus grand (par exemple r10), nous aurions à effectuer de nombreuses fois exactement les mêmes calculs. On pourrait même imaginer si nous avions à notre disposition des barres de 100 m de long, un nombre de calculs à effectuer qui arriverait aux limites des capacités de nos ordinateurs (calculs très longs à effectuer).

Nous sommes donc typiquement dans le cas où la programmation dynamique pourrait nous être utile afin d'éviter de refaire un grand nombre de fois exactement les mêmes calculs.

6) En vous inspirant de ce qui a été fait dans le cours (suite de Fibonacci et rendu de monnaie), écrivez un programme permettant de calculer rn. Ce programme devra utiliser la programmation dynamique.