Formation
Formation . Partage de bonnes pratiques . formation au numériqueTranche de formation toi-même ! (chapitre 11 : le plus court chemin… quelques éléments algorithmiques)
Pour naviguer dans les slides : cliquer, glisser, ou encore ← → au clavier.

Chapitre 11 Slide 0
Que doit faire un GPS ? Souvent, les participants vont répondre qu´il doit vous permettre de trouver un chemin (le plus court possible ou celui qui va le plus vite, ou qui évite les péages, etc.) entre deux lieux.

Chapitre 11 Slide 1
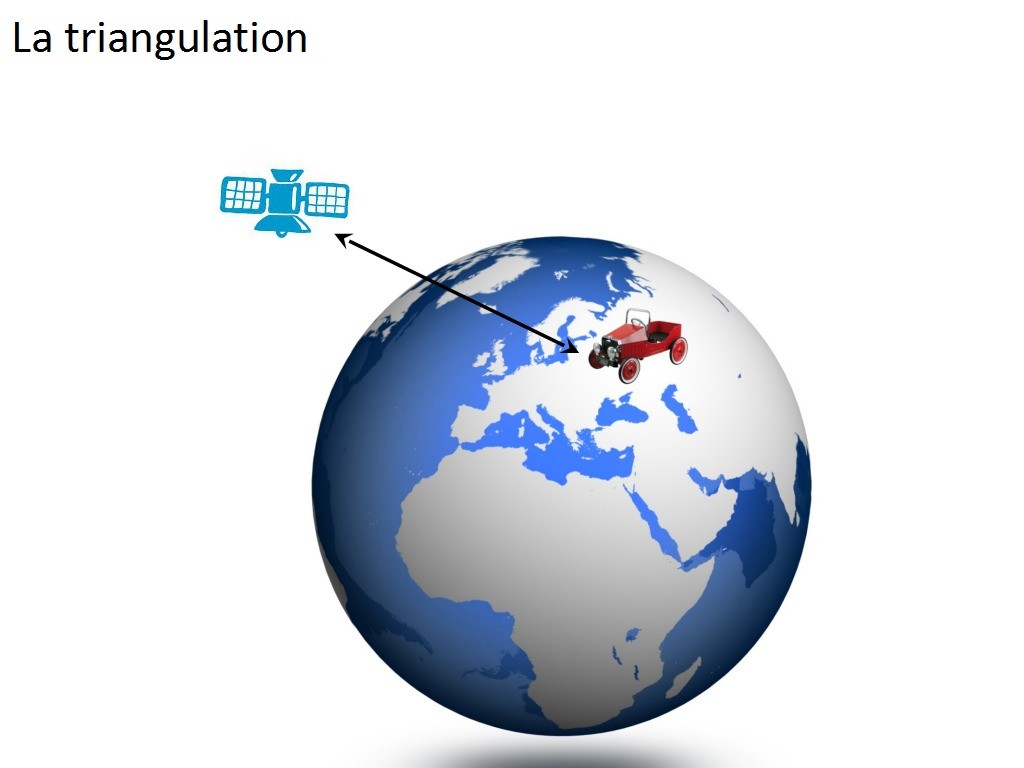
Selon le temps disponible, j´aime bien faire un détour par l´étape "triangulation" car ce n´est pas toujours évident et ça permet de limiter les fausses idées à ce sujet. Donc la triangulation c´est un mot qu´on entend parfois dans les films policiers du genre "ça y est, on a triangulé la position du méchant, on lui tombe dessus, on le met en prison, bien fait, il avait qu´à pas faire le mal ! ".
Chapitre 11 Slide 2
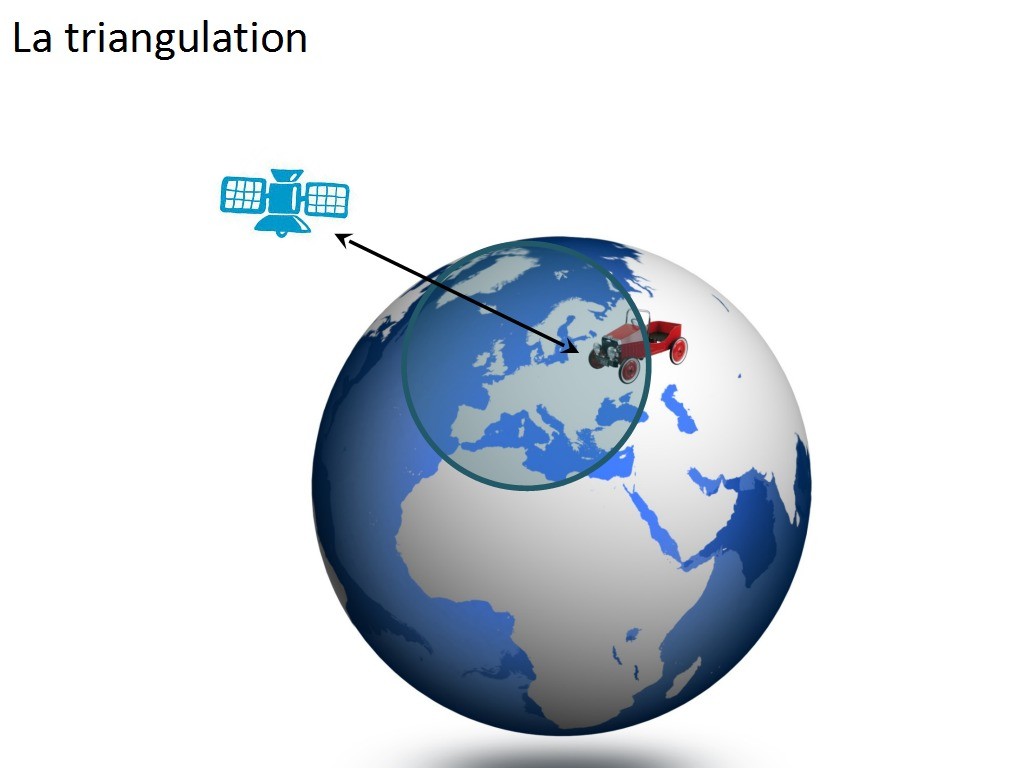
en fait, le GPS peut déterminer votre position grâce aux satellites. Mais le satellite ne donne pas au GPS sa position sur terre ! C'est un système d'horodatage qui permet au GSP de déterminer la distance à laquelle il se trouve du satellite. Ensuite il peut affirmer une chose à coup sûr : il est à l´intersection de deux sphères. La première sphère c´est le globe terrestre. Et la deuxième sphère, c´est celle qui est matérialisée par la distance au satellite (imaginez une ficelle autour du satellite, dont la longueur serait la distance en question, et faites tourner cette ficelle dans tous les sens autour du satellite et vous obtiendrez... une sphère). Notre GPS est donc quelque part sur la première sphère (la terre) et aussi quelque part sur la deuxième (à cette distance du satellite). Il est donc à la périphérie un disque (à l´intersection des deux sphères, et à la surface).
Chapitre 11 Slide 3
Ah oui, mais alors être sur un disque... ça n´est pas très précis...
Chapitre 11 Slide 4
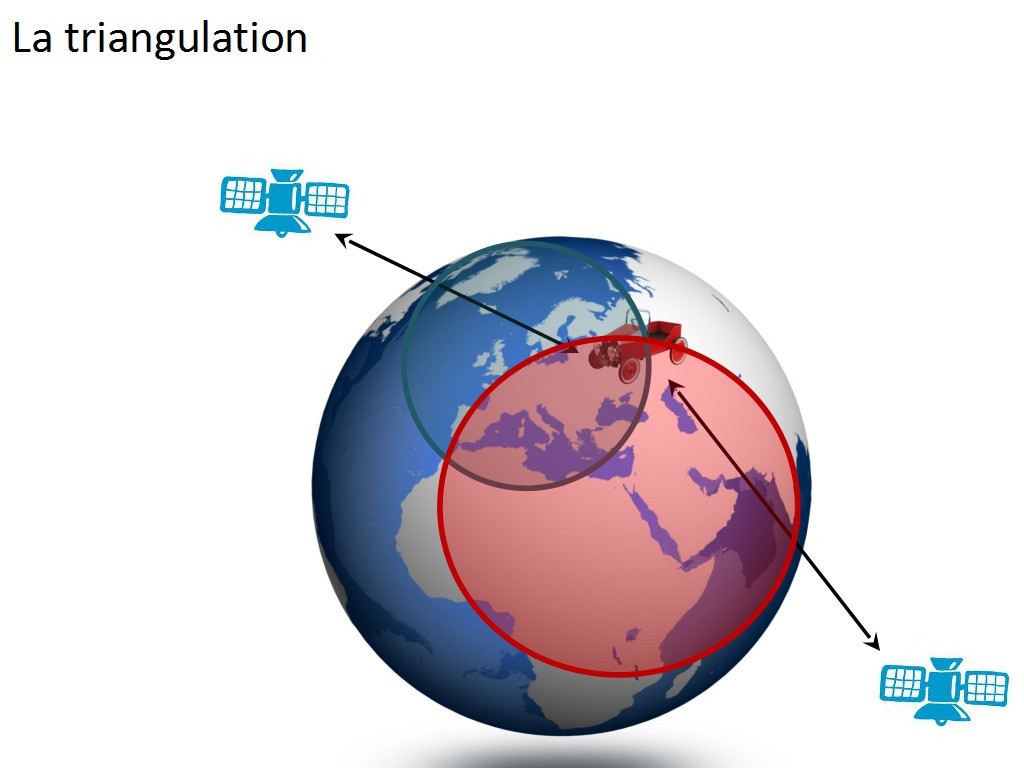
Alors il faut un deuxième satellite. Et cette fois, notre GPS sait qu´il est à l´intersection de trois sphères (donc l´intersection de deux disques), donc il n´y a plus que deux points possibles cette fois. Mais ce n´est toujours pas assez précis (là on peut être en Europe comme en Afrique du nord).
Chapitre 11 Slide 5
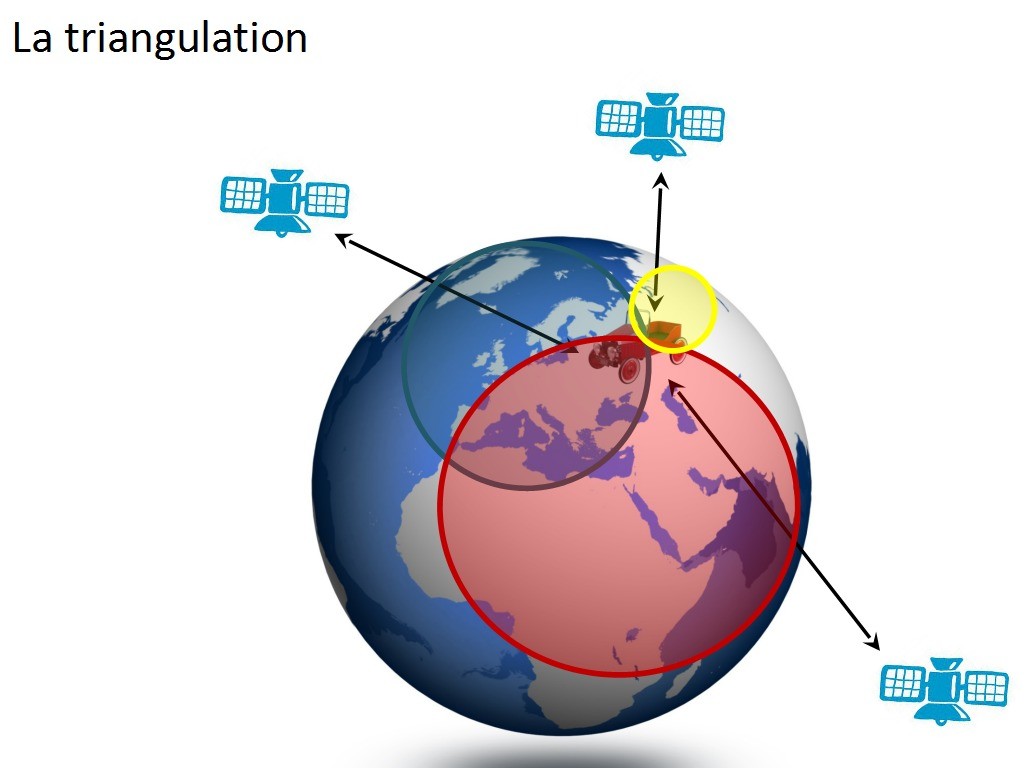
en ajoutant un troisième satellite on peut enfin déduire la position du GPS. Ce troisième satellite est le troisième point dont on a besoin pour se situer. C´est le TROISième dans la TRIangulation. Et on peut en ajouter d´autres, pour plus de précision. Pour aller plus loin : la technique pour le GPS est la trilatération, qui est différente de la triangulation https://fr.wikipedia.org/wiki/Global_Positioning_System

Chapitre 11 Slide 6
passons rapidement sur le fait que le GPS doit aussi afficher la carte et permettre de visualiser sa position...

Chapitre 11 Slide 7
... et la troisième chose que doit faire un GPS c´est de vous proposer un chemin. Par exemple, ici, je veux aller de Montpellier à Marseille.
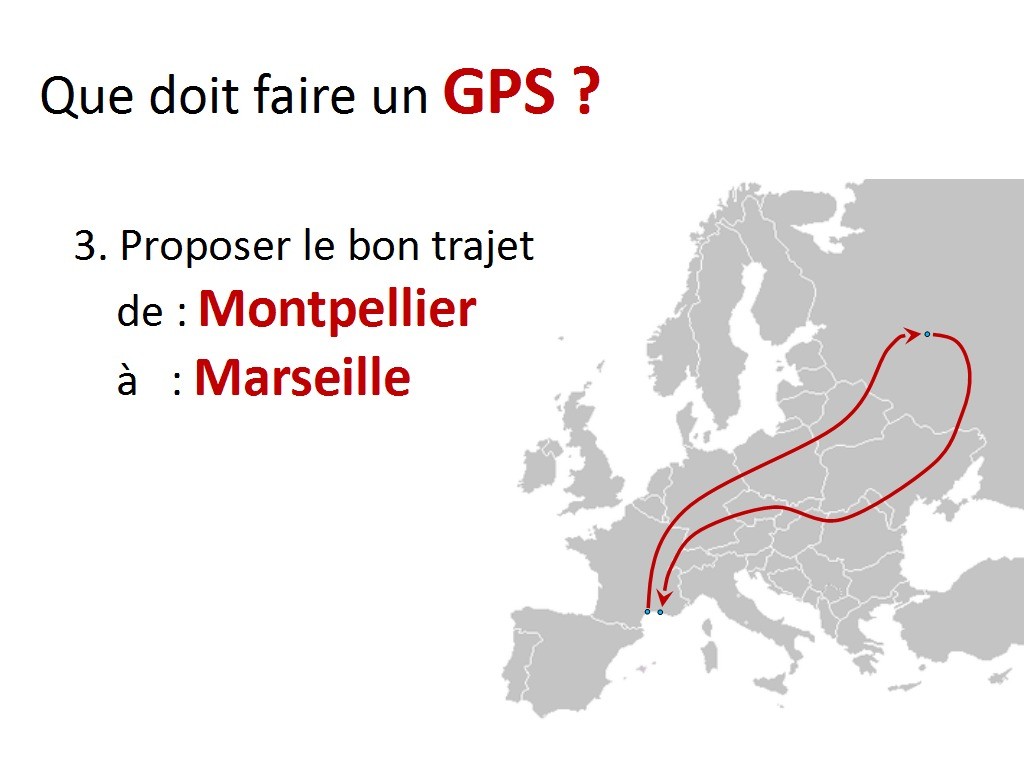
Chapitre 11 Slide 8
"pas de problème" me répond fièrement mon GPS ! Voilà un chemin ! Quoi ? Y a un problème avec ce chemin ? Bon il est peut-être un peu long mais... c´est joli Moscou en même temps... on visite... Bien entendu, l´objectif ici est de mettre l´accent sur "le plus court chemin". Mais est-ce que c´est facile de trouver le plus court chemin. Si je ne donne pas à mon GPS l´algorithme qui permet de le faire, il n´aura aucune méthode. Je peux très bien lui donner l´algorithme facile : "fait avancer ta ficelle parmi les clous et si tu tombes sur la ville de destination alors c´est bon ! ". Mais dans ce cas... je peux y passer des années et mon chemin sera... exotique ! Donc on doit donner à notre GPS un algorithme pour trouver ce plus court chemin. Pour un humain, il est assez rapide de trouver un chemin satisfaisant. On se dit qu´on va passer par ce point, puis prendre cette autoroute et peut-être passer par ce village parce que c´est un raccourci. C´est une manière intuitive de déterminer son chemin. Mais la machine n´a pas d´intuition. Il faut lui donner un algorithme.
Chapitre 11 Slide 9
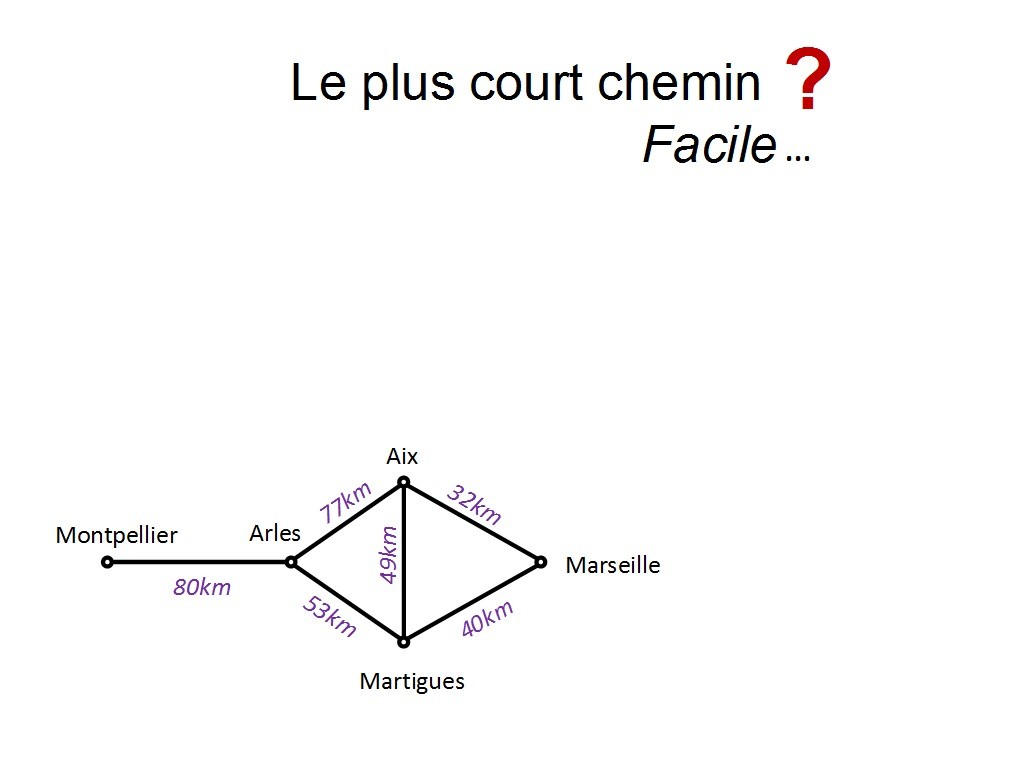
Alors regardons de plus près si ce problème est facile ou pas... Pour aller de Montpellier à Marseille, j´ai le choix. Je peux passer par Aix en Provence (avec l´autoroute) ou par Martigues et voir un peu la mer sur la route. Quel est le chemin le plus court ?
Chapitre 11 Slide 10
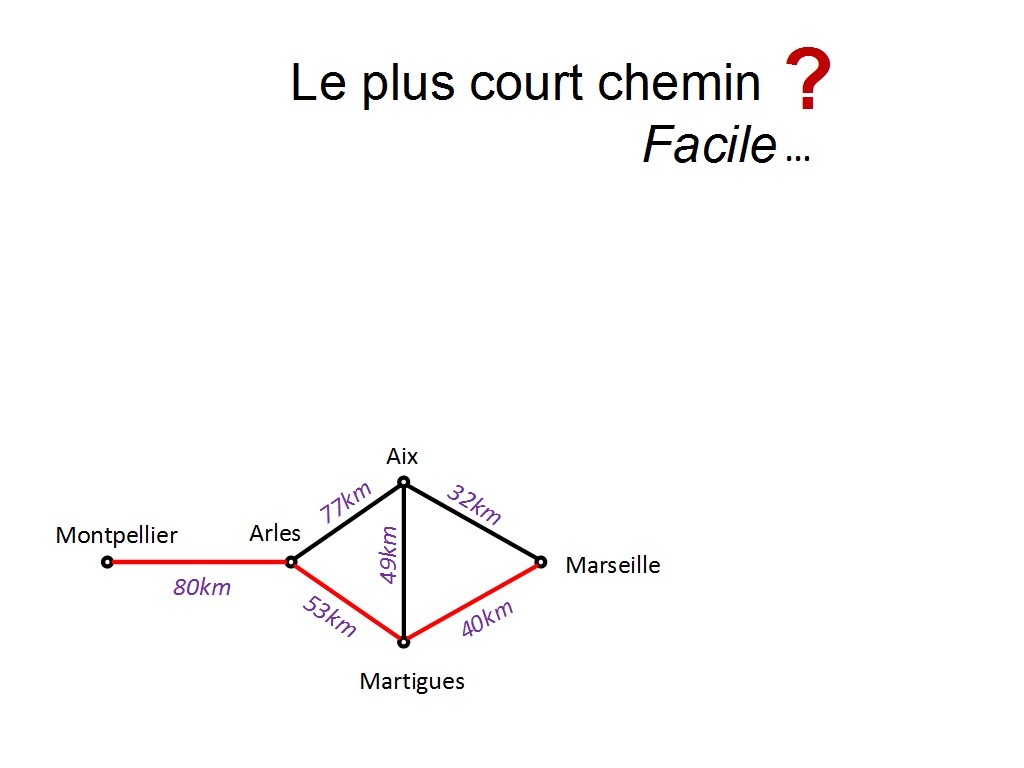
C´est celui qui passe par Martigues. Ok. Mais pour arriver à cette conclusion, combien de chemin fallait-il comparer ? Je laisse un peu les participants faire le calcul et proposer...
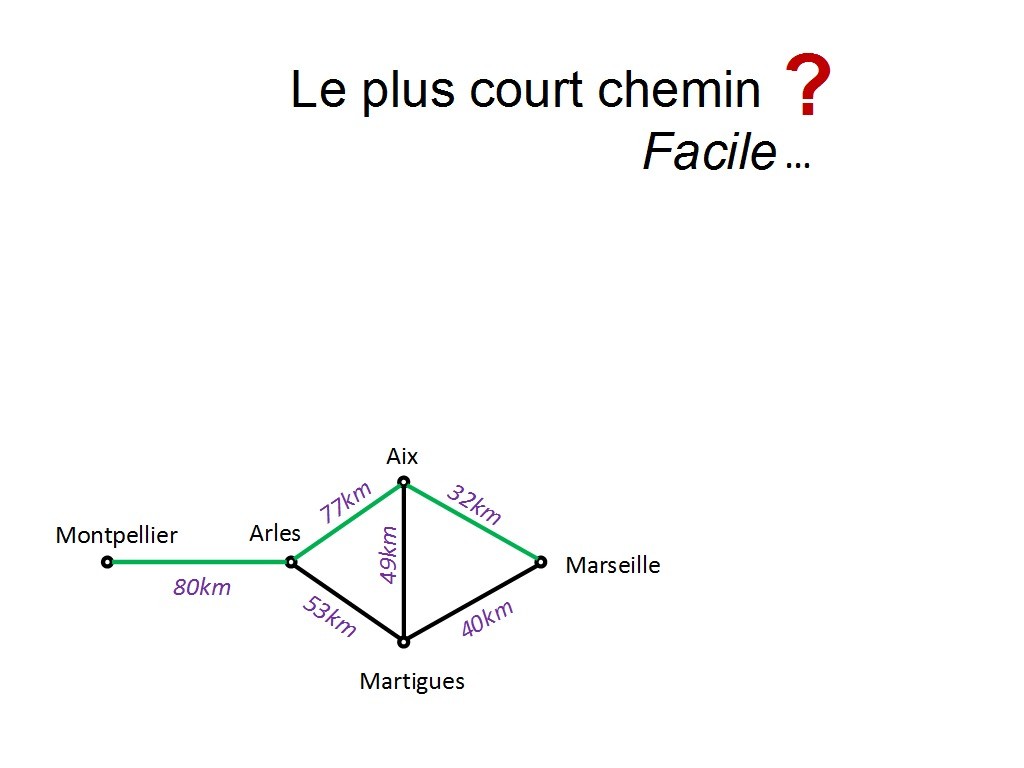
Chapitre 11 Slide 11
il y en a 4 en tout.
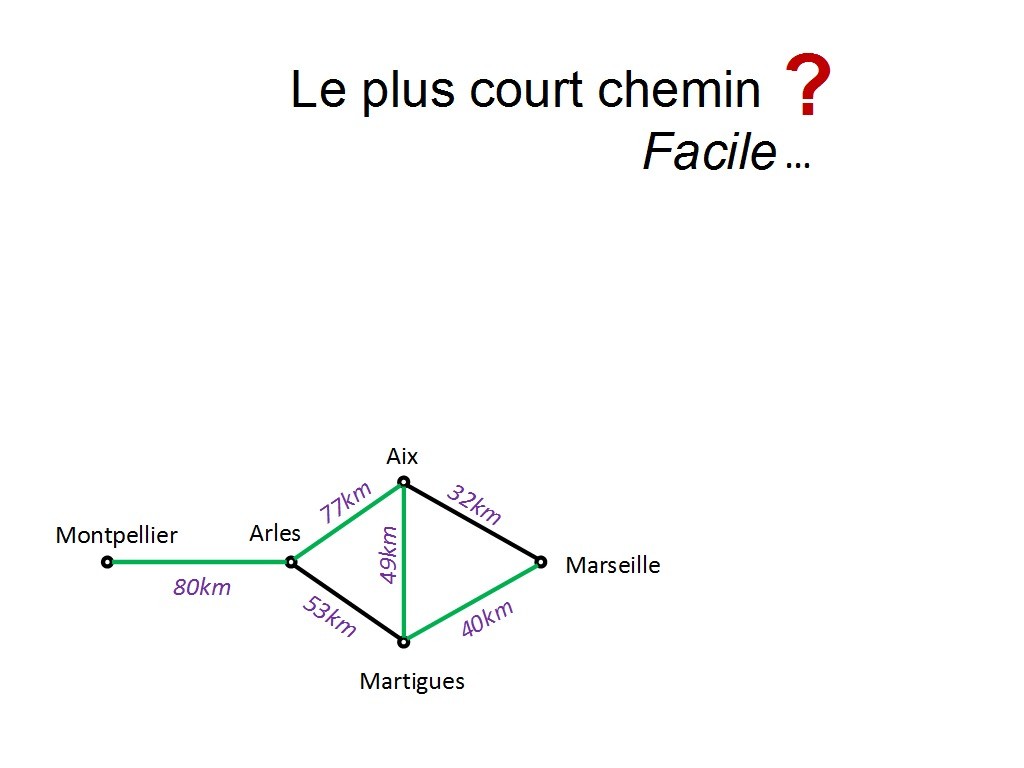
Chapitre 11 Slide 12
il y en a 4 en tout.
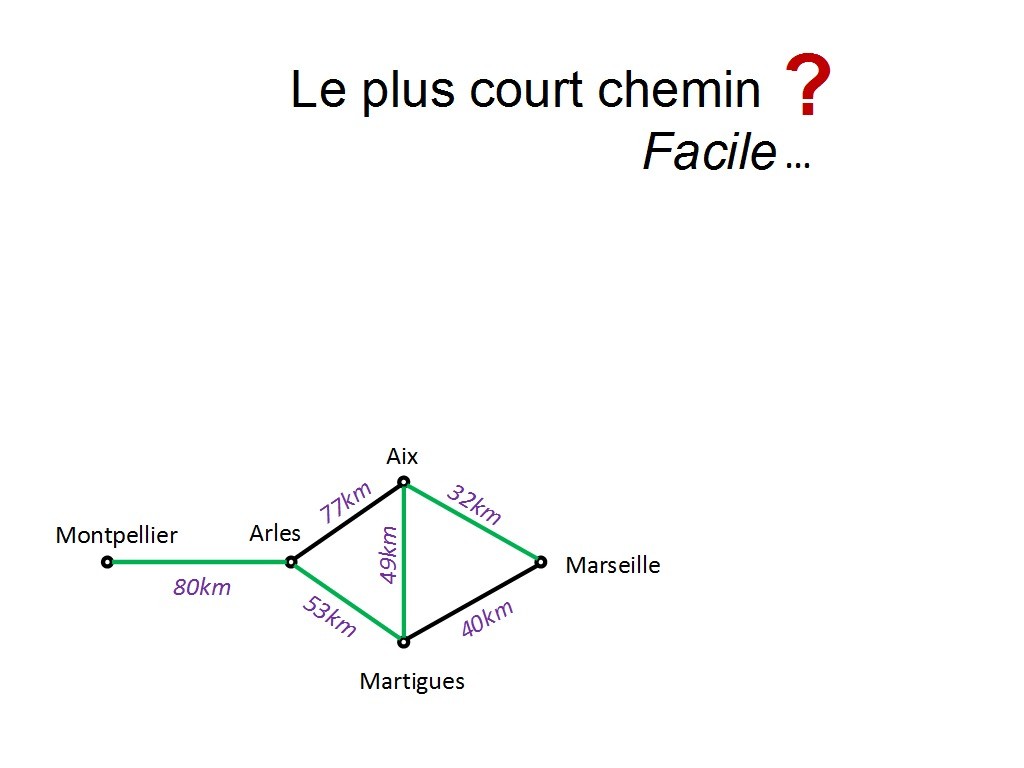
Chapitre 11 Slide 13
il y en a 4 en tout.
Chapitre 11 Slide 14
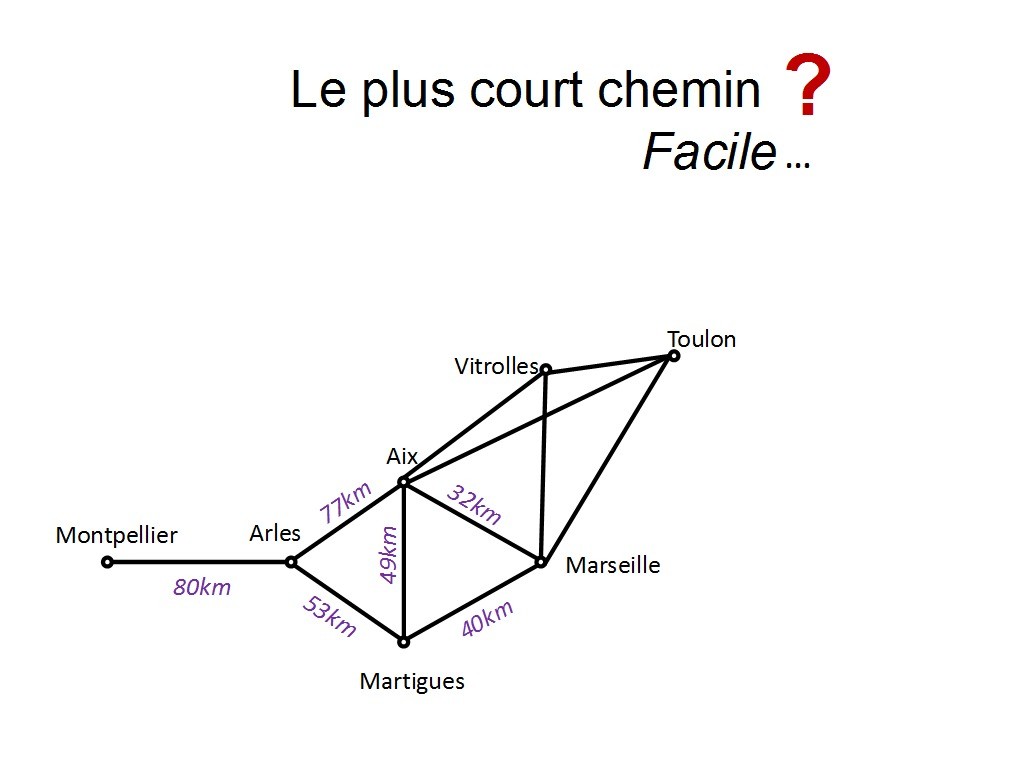
très bien, jusqu´ici c´était simple... Mais si j´ajoute seulement deux villes... combien y a-t-il de chemins possibles maintenant ? Pendant que les participants hésitent entre "c´est trop long, je ne vais pas calculer ça" et "attend, je suis certain que je peux le faire", je coupe court en disant "bon, on va formaliser un peu tout ça pour se faire une idée générale sur la question".
Chapitre 11 Slide 15
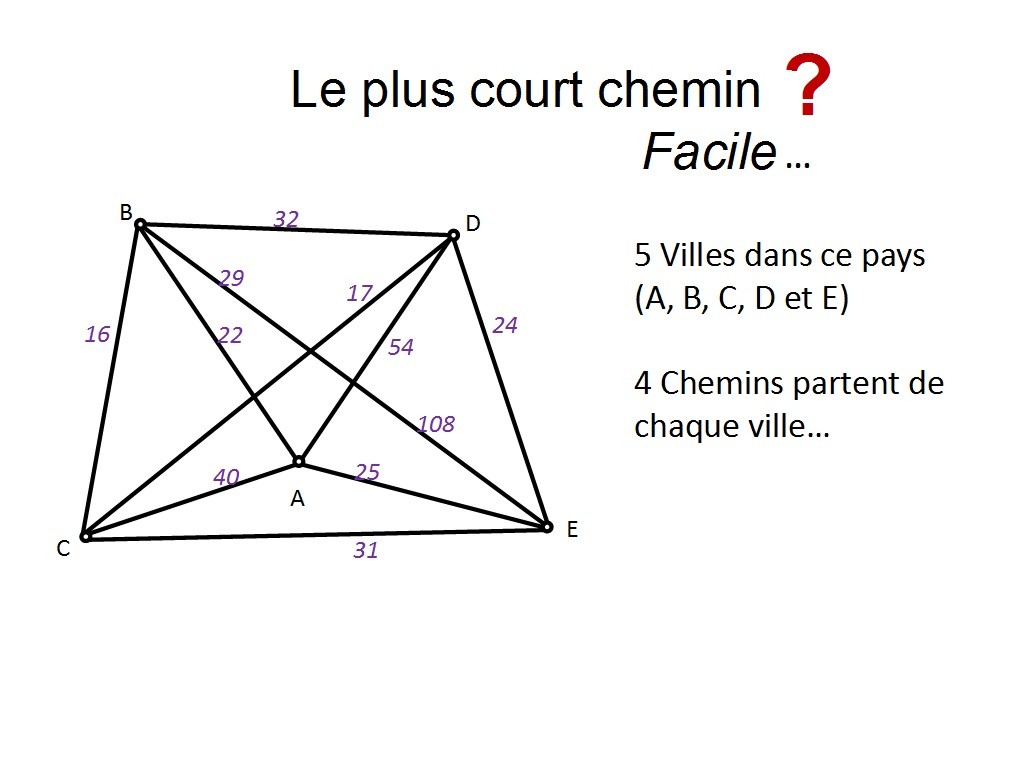
Je vous présente un pays dans lequel il y a 5 villes : A, B, C, D et E (excusez le manque d´originalité). Et un chemin est direct entre deux villes (par exemple, au croisement des chemins entre A-B et C-D il n´y a pas d´intersection, ces deux chemins sont indépendants, on ne peut pas emprunter le chemin depuis A vers B et en croisant l´autre chemin décider qu´on va vers C). Je précise toujours cela, car il arrive régulièrement que des participants se posent la question. Alors autant anticiper. Quand les chemins se croisent, il faut imaginer un petit pont qui dit "on ne change pas de route" 😉 .
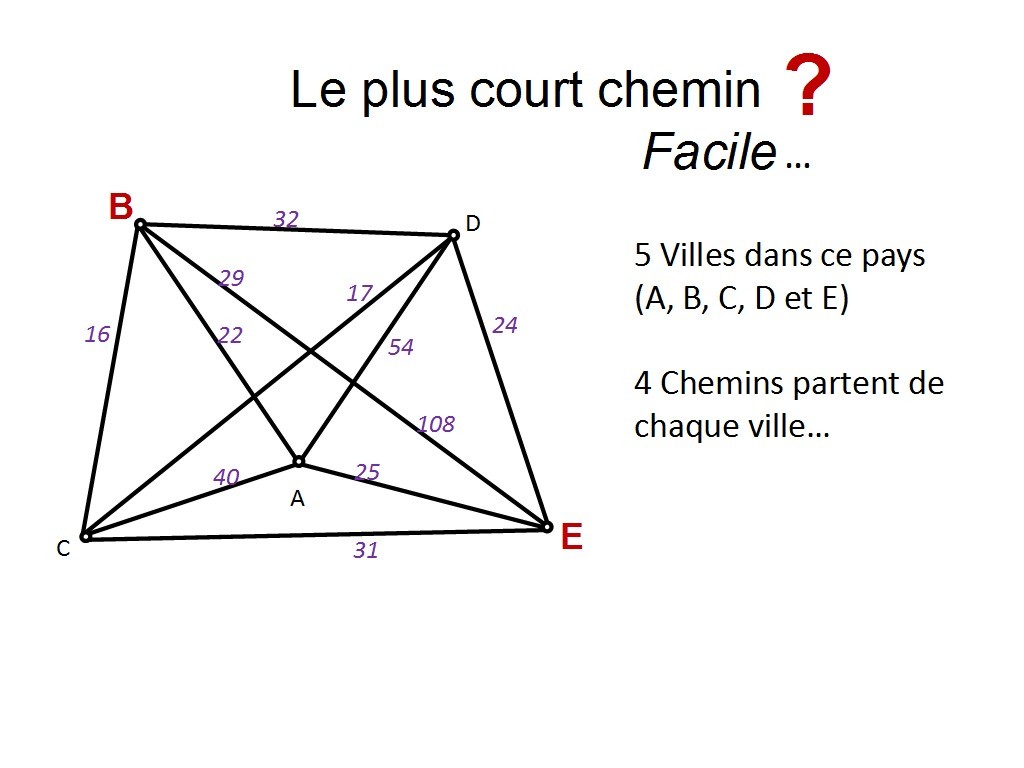
Chapitre 11 Slide 16
Donc, de chaque ville, il y a 4 chemins qui partent. Et je veux aller de la ville B à la ville E, en passant par toutes les autres villes. On va voir combien de chemins cela représente... Combien de départs possibles a-t-on, à partir de la ville B ?
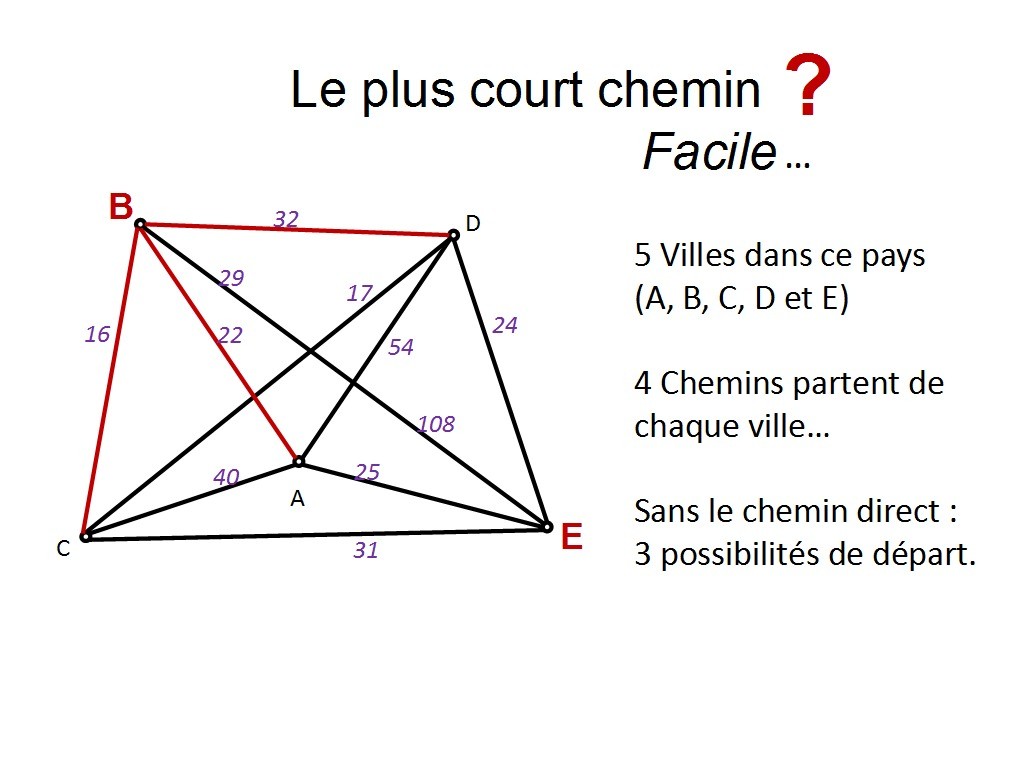
Chapitre 11 Slide 17
Il y en a 3 ! On ne veut pas aller directement sur E, parce qu´on veut passer par toutes les villes, donc E sera notre tout dernier choix. Donc on a 3 possibilités : D, A et C.
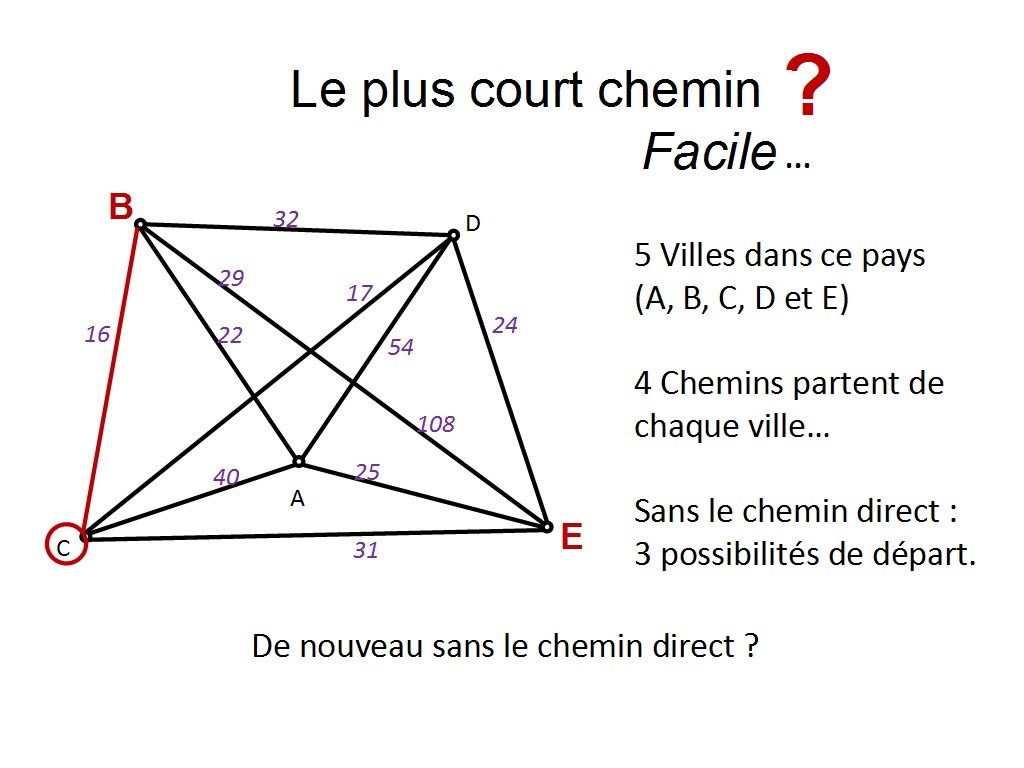
Chapitre 11 Slide 18
Prenons en une au hasard... disons C ! Combien de départ possible à partir de C ?
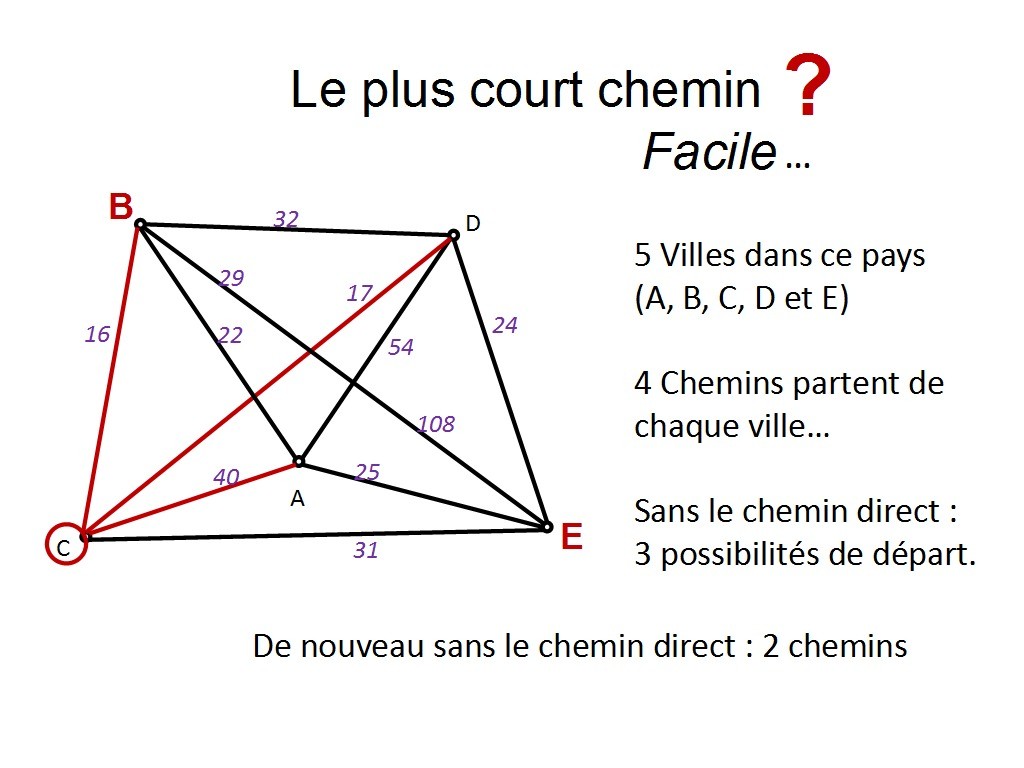
Chapitre 11 Slide 19
Il y a deux départs possibles : D, et A (on évite toujours E).
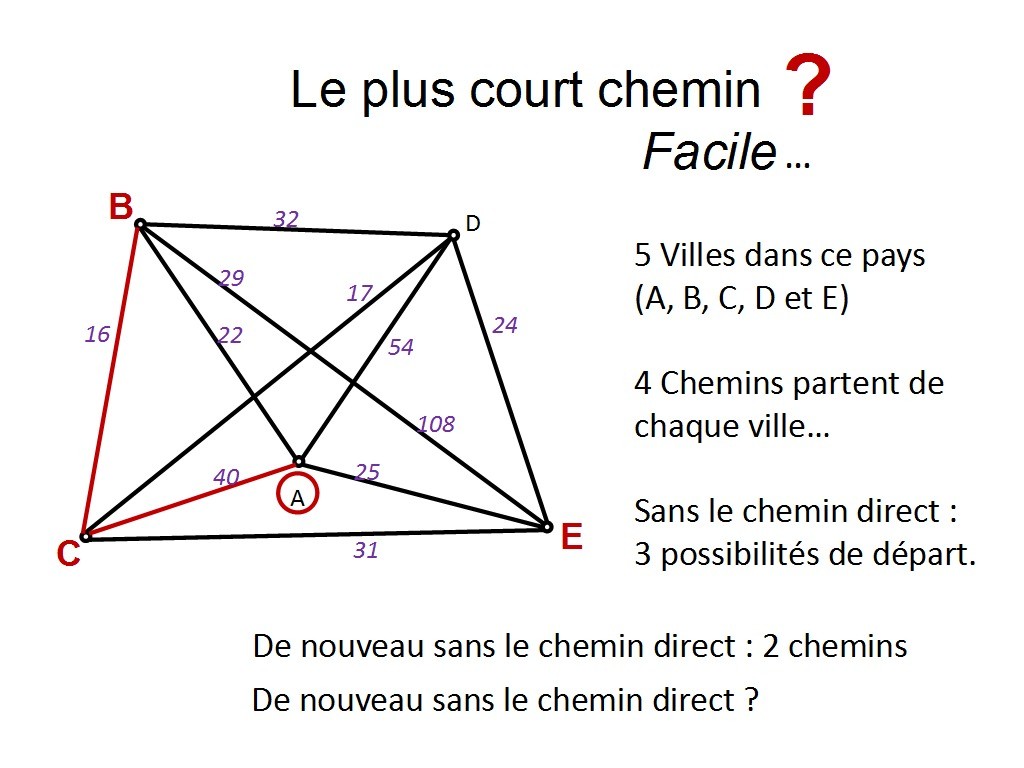
Chapitre 11 Slide 20
On prend A. Combien de départs possibles ?
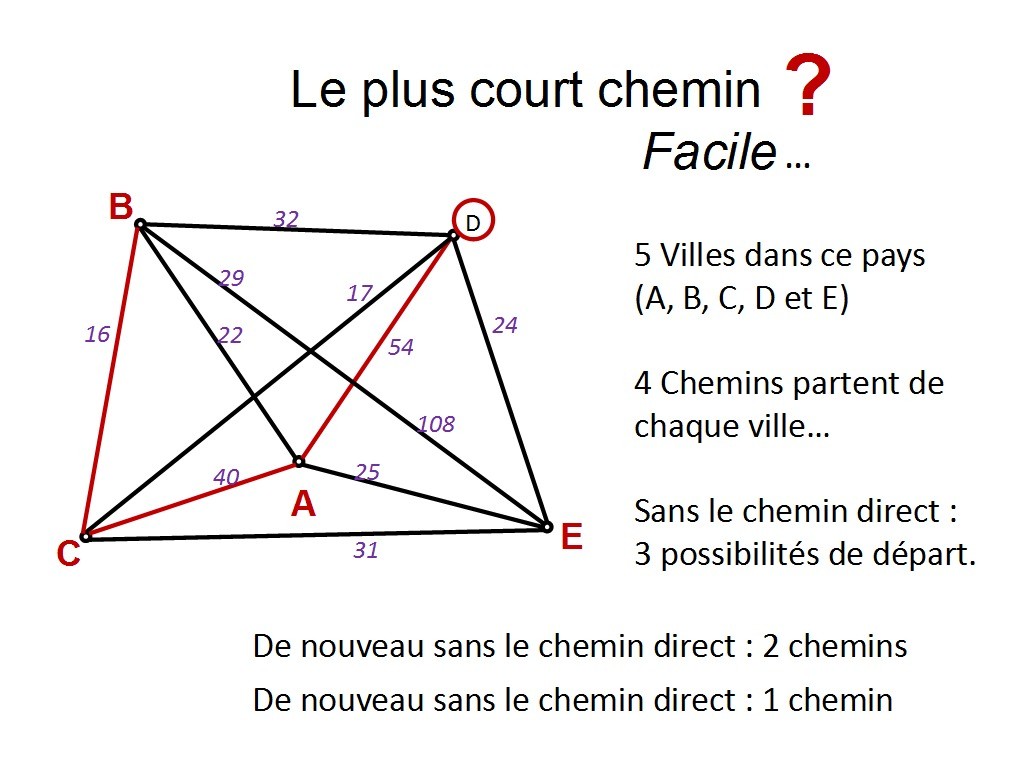
Chapitre 11 Slide 21
Il n´y a plus qu´un seul départ : celui vers D (toujours parce qu´on évite E, ville de destination).
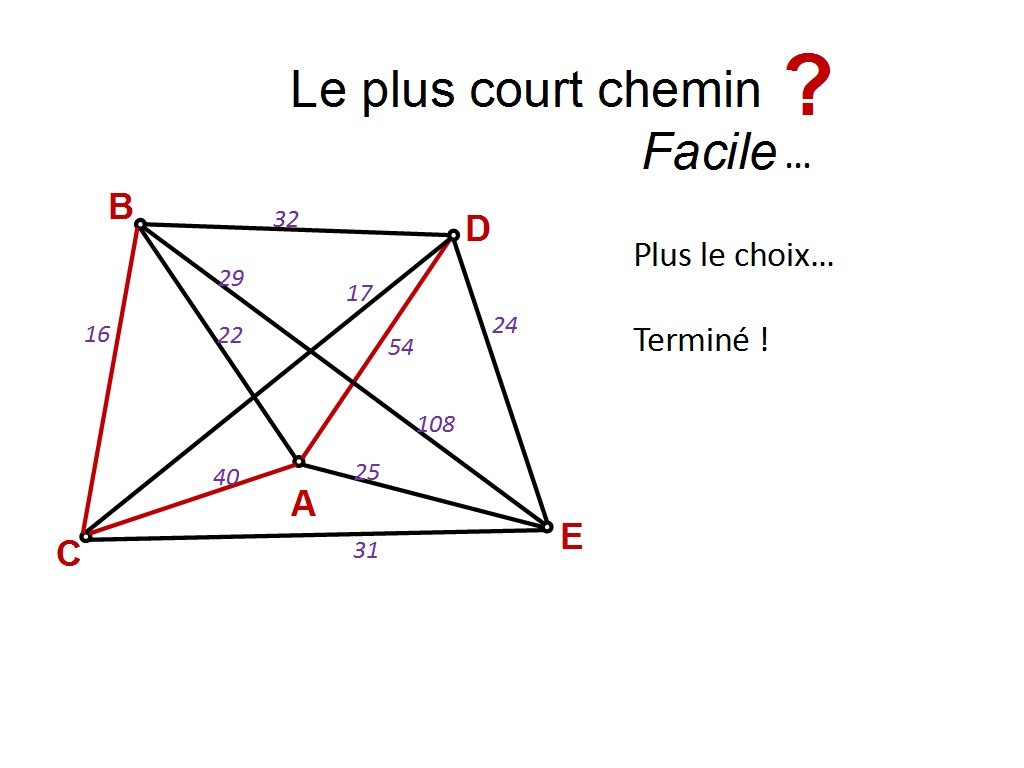
Chapitre 11 Slide 22
C´est terminé, il n´y a plus d´autre choix que E maintenant.
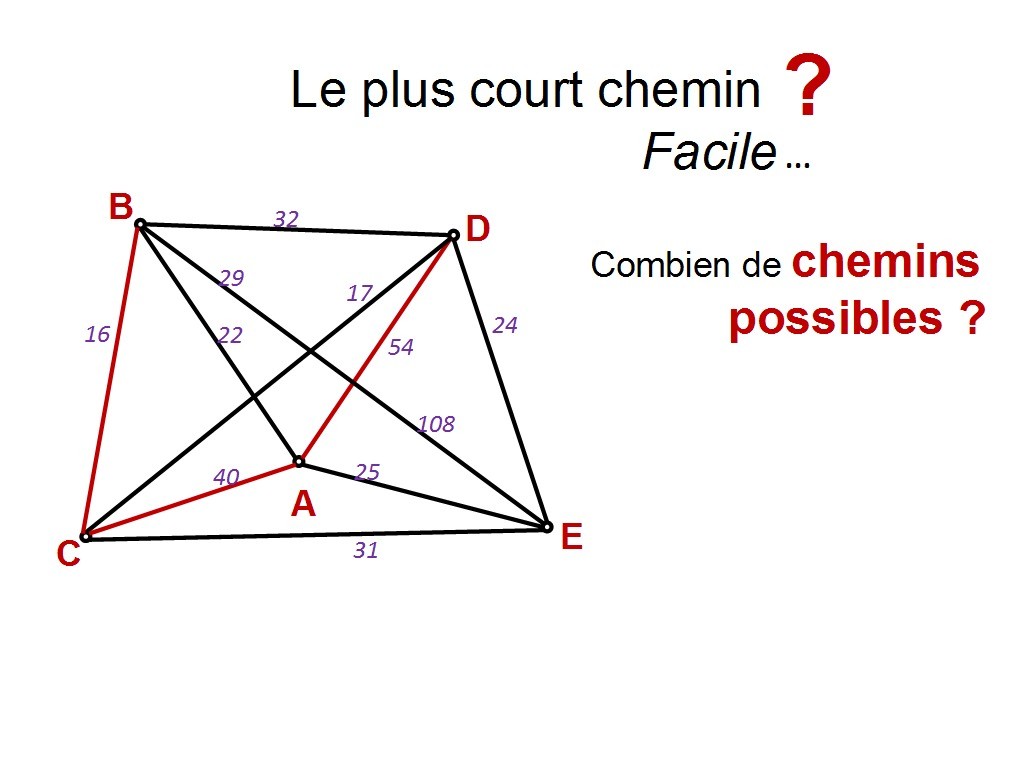
Chapitre 11 Slide 23
Alors faisons un bilan. Combien y a-t-il de chemins possibles, entre B et E ?
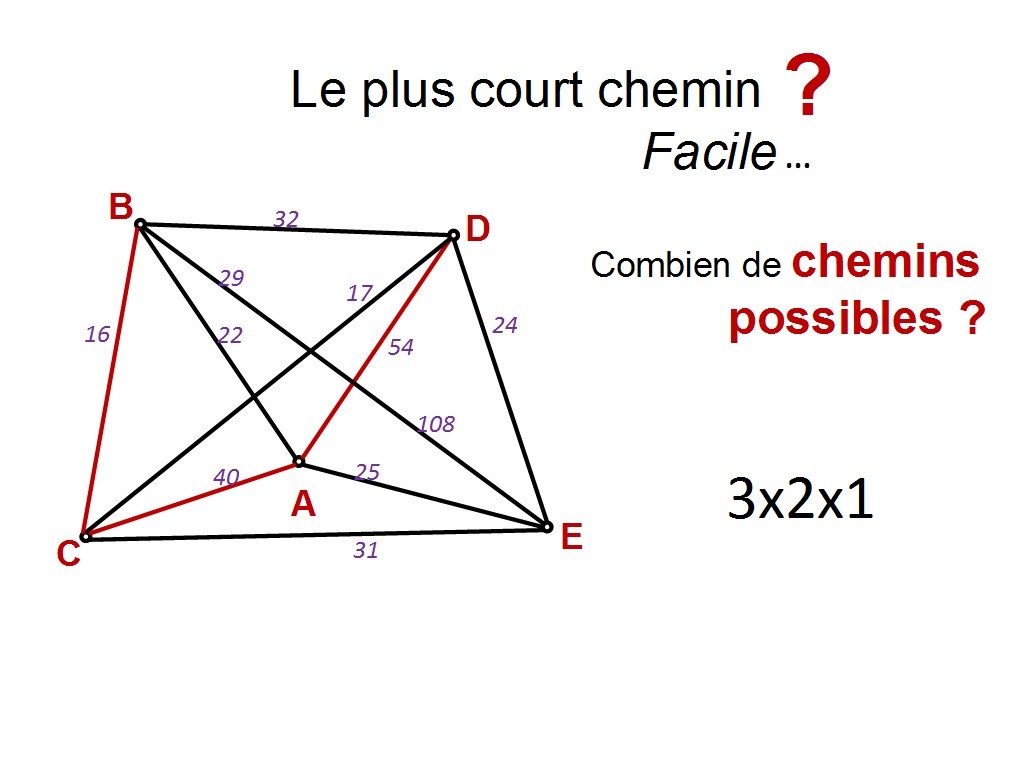
Chapitre 11 Slide 24
il y en a 3 (le nombre de départs possible depuis B) fois 2 (nombre de départs depuis la deuxième ville, quelle qu´elle soit) fois 1 (nombre de départs depuis la troisième ville). Je ne précise pas à l´oral pourquoi "au moins", mais c´est parce qu´on fait le calcul sans les boucles (qui peuvent agrandir ce nombre).
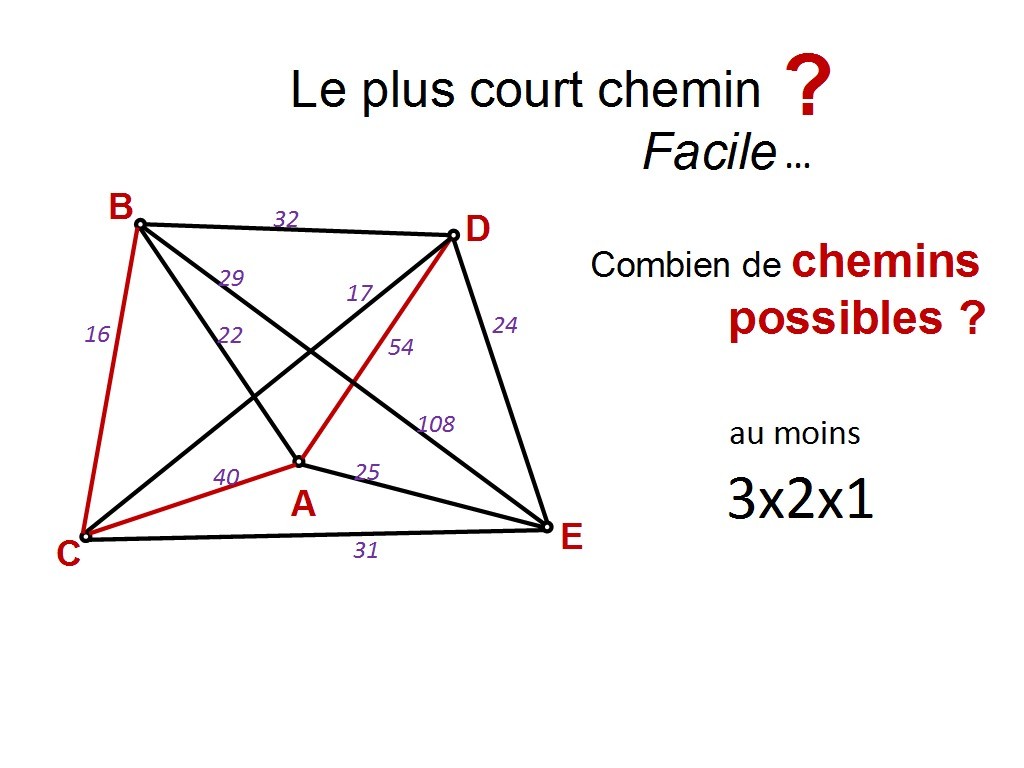
Chapitre 11 Slide 25
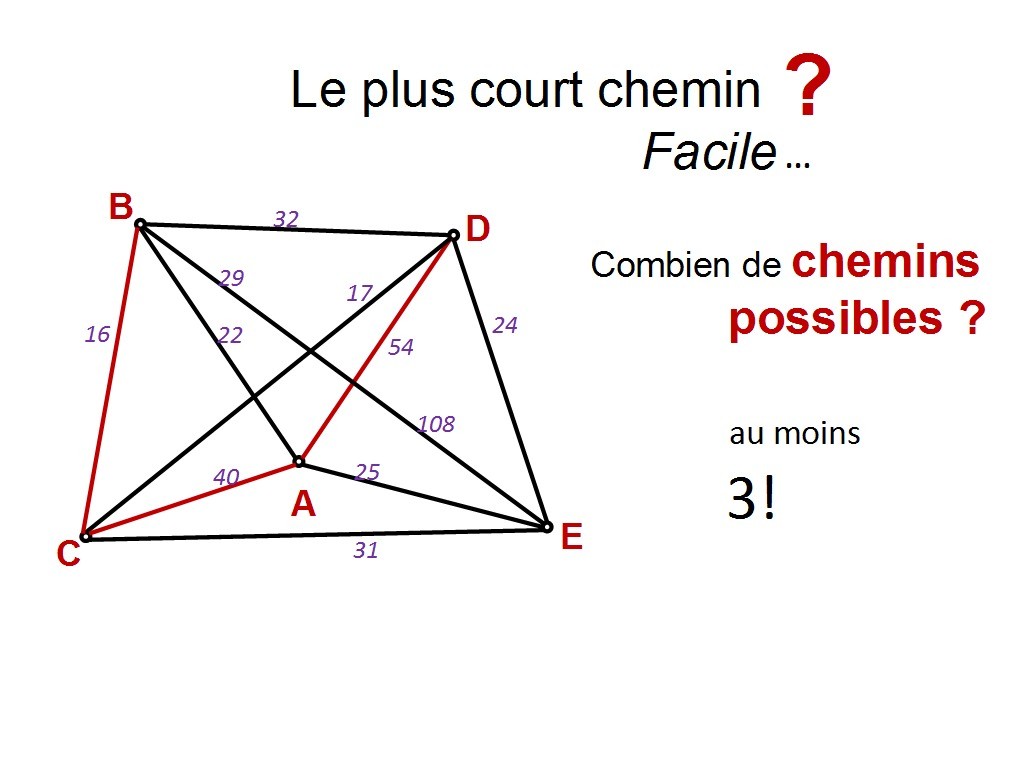
Chapitre 11 Slide 26
on va formaliser tout ça. 3x2x1 on appelle ça une factorielle. Donc on a factorielle 3 chemins possibles.
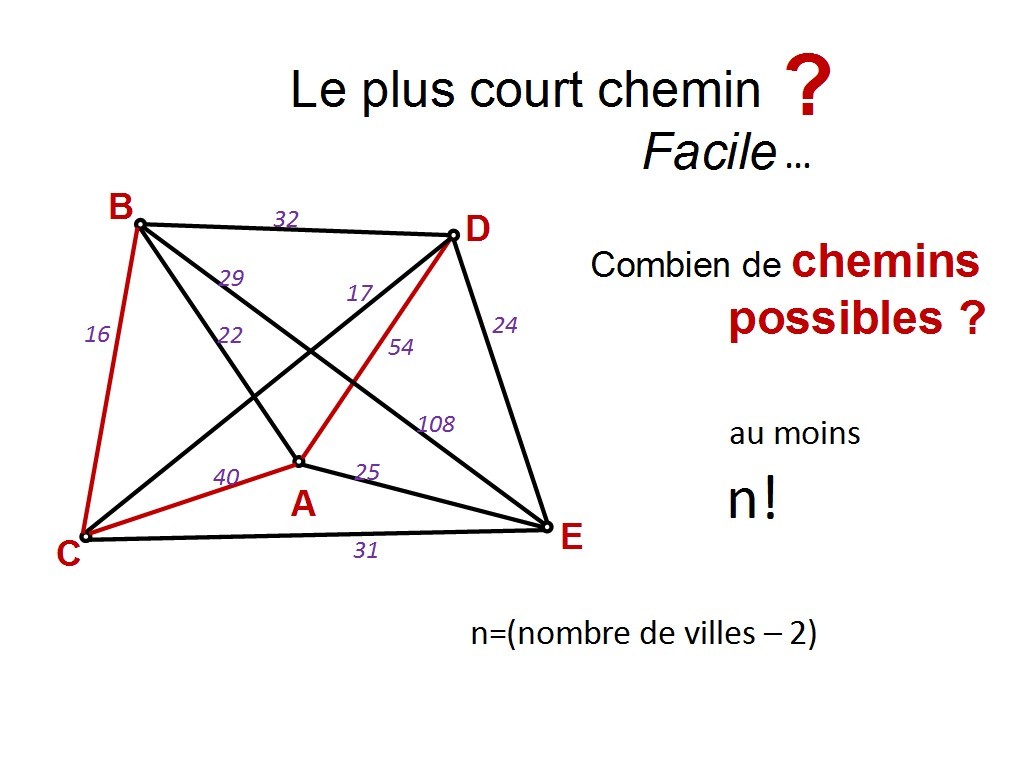
Chapitre 11 Slide 27
On peut même aller plus loin et dire que si on a n=(le nombre de villes - 2) alors le nombre de chemins possibles est de factorielle n. Pourquoi (nombre de villes - 2) ? Parce qu´on a enlevé la ville de départ, et la ville d´arrivée.

Chapitre 11 Slide 28
donc en fait, quel que soit le nombre de villes dans ce pays, le nombre de chemins possibles est au moins de factorielle n.

Chapitre 11 Slide 29
maintenant qu´on a fait tout ça et qu´on peut estimer ce nombre de chemins quel que soit le nombre de villes, profitons-en pour faire quelques essais. Avec les 5 villes de mon micro pays (A,B,C,D,E) on a donc 6 chemins possibles. Avec 20 villes, ce qui correspond à la planche à clous de l´activité précédente, d´après vous, combien y a-t-il de chemins possibles ? Cette étape est importante et il faut bien veiller à aider les participants s’ils montrent des difficultés. En général, j´essaie de leur faire expliciter le calcul. Par exemple voir que n=18 (nombre de villes - 2) et donc le résultat qu´on cherche est factorielle n. Ensuite, ils se disent "c´est 18x17x16 etc.". Oui ! C´est vrai ! Et alors d´après vous ça fait combien ? Parfois, surtout avec les Lycéens, il y en a un(e) qui sort sa calculatrice pour lancer le fameux "18x17x16 etc." et, de manière amusante, jusqu´ici jamais aucun n´a tapé "18!" sur sa calculatrice. Donc pour tout taper ça lui prend une temps fou ! Bref, continuons avec la question posée aux participants : combien ça fait, d´après vous, factorielle 18 ? Pour ne pas qu´ils se sentent en situation de test, du genre "je te juge et si tu te trompes c´est la honte" je leur dis "allez-y, n´hésitez pas, moi la première fois que j´ai essayé d´estimer ça je suis tombé à des années lumières du résultat, donc vous ne pourrez pas faire pire que moi ! ! ". Ils diront parfois "des milliers"... parfois "des millions" et même "des milliards"...

Chapitre 11 Slide 30
Il y en a plus de 6 millions de milliards !! (dit avec un ton dramatique, ça fait toujours son petit effet 😉 ). "Ah oui ! ! C´est bien ça ! ! ", s´exclame à ce moment l´élève qui vient de terminer de rentrer "18x17x16x(...)x2x1" sur sa calculatrice quand j´utilise ces slides dans une école 😛 .

Chapitre 11 Slide 31
Il est temps de conclure sur ce passage. Finalement ce qui paraît assez intuitif pour l´humain, devient particulièrement gourmand sur une machine. L´algorithme qui consiste à énumérer tous les chemins possibles pour en retenir le plus court ne peut tout simplement pas être exécuté sur un GPS... ce serait beaucoup trop long. Donc ce que fait un GPS, c´est un peu ce que vous avez fait tout à l´heure avec l´activité de la planche à clous. Son algorithme consiste à jeter une ficelle, puis à améliorer son chemin par endroits et au bout d´un moment, quand les améliorations sont très petites, ou bien qu´il n´y en à plus, il renvoie le résultat. Pour se donner plus de chances de trouver un chemin convaincant, il peut aussi lancer plusieurs ficelles en parallèle et prendre le meilleur résultat. Mais il ne donnera pas le "vrai" plus court chemin. Il ne peut pas le garantir. Il trouve le chemin qui est le plus acceptable, avec la technique des ficelles. Mais ce passage est aussi l´occasion d´une réflexion qui me paraît cruciale sur l´algorithmique (merci à monsieur Jean-Paul Bordat, mon prof d´algo en Licence d´informatique à Montpellier, qui fut le premier à me parler des milliards d´années que peut prendre un algorithme pour s´exécuter sur une machine, si on ne prête pas attention à sa complexité). Alors imaginons maintenant... imaginons qu´on dispose d´un GPS qui est capable de calculer ces 6 millions de milliards de combinaisons en une minute. Il peut donc me dire, en une minute, quel est le plus court chemin pour me rendre d´une ville à une autre en passant par toutes les villes. Une minute ça va... c´est raisonnable... mais imaginons maintenant qu’une nouvelle ville se construise dans ce pays. On passe donc à 21 villes. Le GPS va mettre combien de temps pour me répondre maintenant ? Je laisse alors les participants réfléchir à la question pour finalement arriver à la conclusion qu´il lui faudra probablement 19 fois plus de temps. Ce n´est peut-être pas très rigoureux, mais je crois que ça donne une idée de ce qu´est la complexité exponentielle. Alors disons cela, puisqu´en une minute il peut calculer le chemin pour 20 villes en calculant 18x17x16x(...)x2x1 chemins, alors avec une seule ville supplémentaire il mettra 19 minutes. Et avec deux villes supplémentaires, il mettra 19x20 minutes (ce qui fait un peu plus de 6h). L´occasion de réfléchir sur les progrès de l´informatique et de la micro-électronique. On court après les gigahertz et on veut souvent le dernier processeur, le plus rapide. Et heureusement que la micro-électronique fait des progrès énormes pour nous proposer une telle puissance de calcul. Mais ce qu´on voit ici c´est que, même avec de tels progrès, on peut mettre à genou n´importe quel super calculateur avec un algorithme simple, mais naïf. Par exemple un algorithme qui énumère beaucoup (trop) de solutions possibles avant de choisir la meilleure. Il suffit d´ajouter une petite information, comme une ville supplémentaire, et tout s´écroule. Ainsi, les progrès sont nécessaires à la fois en micro-électronique (pour les gigahertz, par exemple) et en algorithmique (pour exploiter au mieux les gigahertz en question).