Formation
Formation . Partage de bonnes pratiques . formation au numériqueTranche de formation toi-même ! (chapitre 3 : la dichotomie et les prénoms)
Pour naviguer dans les slides : cliquer, glisser, ou encore ← → au clavier.

Chapitre 03 Slide 0
Dans la troisième partie de cette formation je demande aux participants de chercher leurs prénoms dans une liste. Autant les prévenir, la liste est prévue pour une génération de Lycéens de 2008... Mais il faut bien chercher quand même car la question sera d´affirmer avec certitude que son prénom est, ou n´est pas, dans la liste. Et la liste sera affichée trois secondes (inutile de dire que les réactions sont assez frustrées après la projection de la liste... "c´est trop court", "c´est pas possible" etc. 😉 ).
Chapitre 03 Slide 1
affichage de trois secondes donc... (juste un conseil : pour compter trois secondes il vaut mieux compter "3, 2, 1, 0" et passer le slide quand arrive le "0", parce que compter "1, 2, 3" et passer le slide quand arrive le 3 ça fait seulement deux secondes 😉 ).

Chapitre 03 Slide 2
Je demande alors aux participants de lever la main si ils peuvent affirmer avec certitude que leur prénom est dans la liste. Il y en a généralement très peu. Je demande aussi d´ajouter leur main levée à ceux qui peuvent affirmer avec certitude que leur prénom n´est pas dans la liste. Il y en a toujours un ou deux qui disent "oui, moi je peux déjà affirmer que mon prénom n´y est pas". C´est souvent le cas du "mon prénom est beaucoup trop original, il ne peut pas y être. Dans ce cas, je m´amuse à leur demander avec fermeté "attention, parce qu´on va revoir la liste, et si ton prénom y est, tu me dois un million d´Euros 😀 ! ". En général, ça suffit à mettre un doute dans l´esprit du participant qui affirme que son prénom n´y est pas et baisse la main. D´autres la maintiennent en étant très sûrs d´eux (et du fait que, quoi qu´il arrive, je n´aurai pas mon million). C´est souvent le cas du prénom très court ou très long.

Chapitre 03 Slide 3
J´annonce alors qu´on va revoir la liste, toujours 3 secondes, mais que cette fois elle sera triée.
Chapitre 03 Slide 4
Affichage de la liste triée

Chapitre 03 Slide 5
Je repose les mêmes questions (qui peut dire avec certitude que son prénom est dans la liste ? Qui peut affirmer que son prénom n´y est pas ?) et là par contre, presque tout le monde lève la main ! "Que s´est-il passé ? ". Et la réponse est bien entendu "c´est plus facile quand c´est trié ! ".

Chapitre 03 Slide 6
Et donc je demande "En quoi ça vous aide, de quelle manière avez-vous cherché votre prénom ?". Et la réponse est à 99% "je cherche la première lettre, puis une fois que je l´ai trouvée, je cherche la deuxième, et la vois rapidement si il y est ou pas". Parmi les 1% restants, on trouve parfois "je cherche plutôt vers la fin, car mon prénom commence par un Z". Et il y a toujours ceux qui ont un prénom très court ou très long.Une variante, qui fait plutôt marrer les participants, c´est de dire qu´un jour un participant m´a dit "moi, mon prénom c´est Pierre-Alexandre-Maxime-Walter donc tu vois... si mon prénom est dans la liste... je le vois tout de suite ! ! 😀 ". Bien entendu, ce n´était pas exactement son prénom (mais pas loin). Et donc c´est également l´occasion de discuter de la recherche plutôt visuelle (pas sur la première lettre, mais sur la longueur du prénom).

Chapitre 03 Slide 7
C´est encore une façon de dire que toute manière de chercher son prénom dans la liste est un algorithme. Un peu comme la stratégie gagnante au jeu de Nim, on peut en faire un programme pour qu´une machine cherche le prénom dans une liste. Et quand on propose un algorithme, on veut montrer deux choses. La première c´est qu´il est correct (il fera bien ce pour quoi il est conçu). La deuxième c´est d´évaluer combien d´instructions (ou d´opérations) il lui faudra pour accomplir sa tâche.

Chapitre 03 Slide 8
Alors prenons un algorithme et testons le... Il s´agit de prendre un prénom au hasard, de le comparer au prénom recherché et de recommencer si ce n´est pas le cas. Est-ce que cet algorithme fonctionne ? Souvent, les participants disent que "oui, mais ça peut prendre du temps". C´est sans compter sur le fait que je suis assez vicieux pour cacher des bugs. Ici, le fait qu´on ne retire pas de la liste le prénom tiré au hasard. Ainsi, si on n´a vraiment pas de chance, on ne le trouvera pas (bien entendu, statistiquement, après plusieurs milliards d´essais sur une petite liste, on va le trouver, mais si la liste fait plusieurs milliards de prénoms, comme la population mondiale par exemple ?).

Chapitre 03 Slide 9
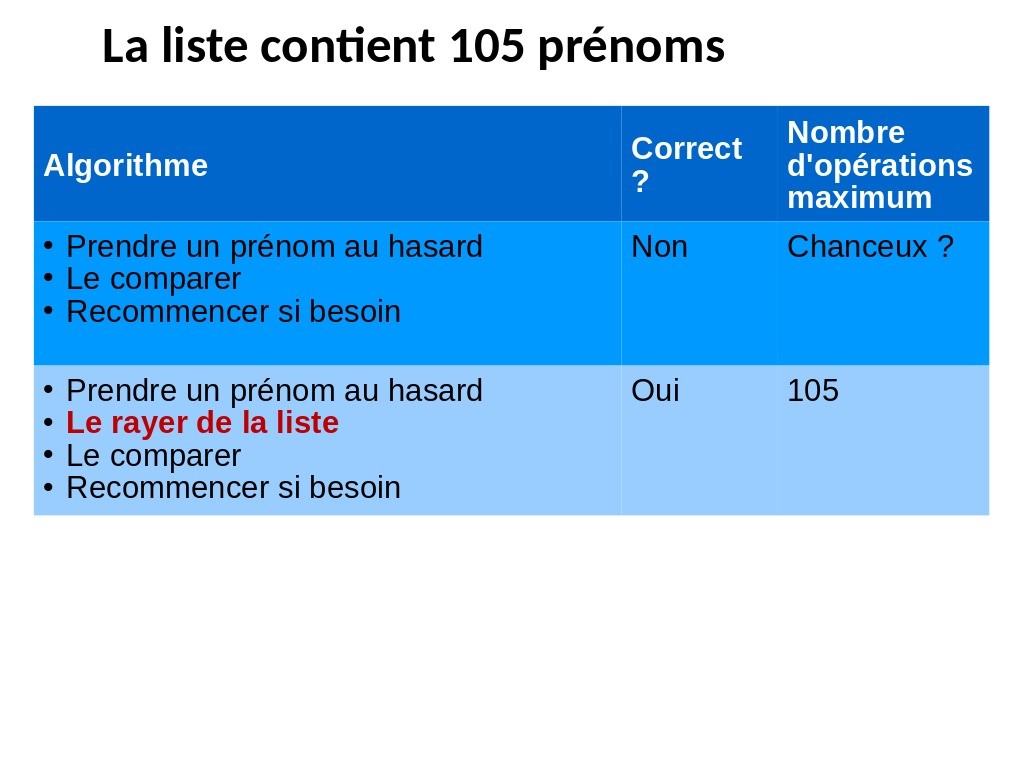
Chapitre 03 Slide 10
Donc la version correcte de cet algorithme, consiste à retirer le prénom de la liste avant de recommencer. Là on sait qu´on va pouvoir affirmer la présence/absence du prénom et on sait également estimer en combien d´opérations. Pour cela on estime le pire des cas. C´est à dire qu´on doit aller jusqu´au dernier prénom. Même si il est dans la liste, on peut ne pas avoir de chance et ce sera le dernier qu´on tire au hasard.
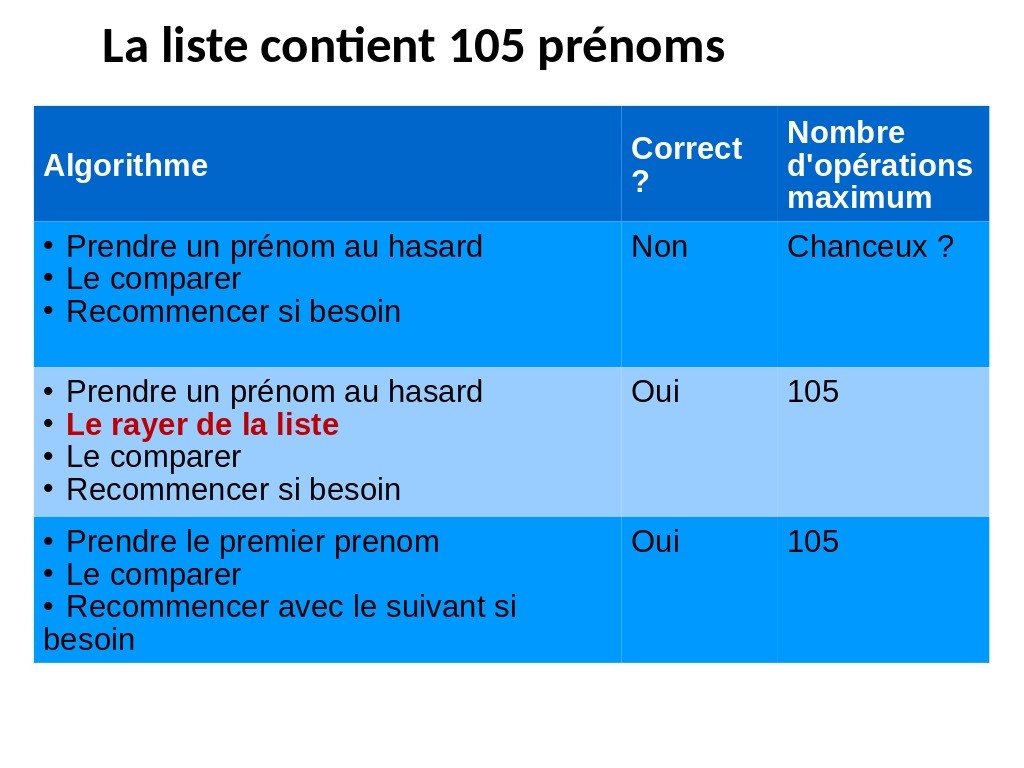
Chapitre 03 Slide 11
Ce qui est intéressant c´est de voir une troisième possibilité pour cette recherche exhaustive : on prend les prénoms du premier au dernier. Et on peut facilement voir que l´algorithme est correct, mais surtout qu´il prend exactement le même nombre d´opérations que l´algorithme qui prend les prénoms au hasard. Dans les deux cas, on peut aller jusqu´au dernier avant de répondre. Tout cela vient du fait qu´on ne tient pas compte, dans ces algorithmes de l´ordre dans lequel les prénoms sont inscrits. Une question peut venir comme "oui, mais si avec l´algorithme qui prend au hasard on tombe dessus du premier coup, c´est bon, on a pas mis 105 opérations, c´est plus rapide que l´autre". C´est l´occasion de parler de complexité en moyenne et dans le pire des cas. En général je réponds que si on utilise ces deux algorithmes 10 000 fois, alors on va constater des performances moyennes similaires pour les deux.

Chapitre 03 Slide 12
Avant de voir comment on peut prendre l´ordre alphabétique en considération, voyons pourquoi le problème peut devenir très difficile et pourquoi il est important de trouver une approche plus efficace. En 2013 (mais aussi 2014 et 2015), il y a eu environ 700 000 candidats au bac. Imaginons que je suis le serveur qui détient la liste des 700 000 prénoms avec l´inscription "oui" ou "non" pour l´obtention du bac. Je vais donc recevoir 700 000 fois la question "est-ce que je suis reçu". Et 700 000 fois, je vais devoir regarder dans une liste de 700 000 prénoms.

Chapitre 03 Slide 13
Cela veut dire que si j´applique un des algorithmes de S12, je vais faire environ 500 milliards d´opérations (ok, en vérité c´est la moitié, parce que la distribution des prénoms, etc... personnellement, je préfère garder ce 500 milliards, plutôt qu´ajouter une information qui ne me semble pas servir le message principal, il ne m´est arrivé qu´une seule fois de devoir préciser que c´est la moitié, sur une vingtaine de fois où j´ai utilisé ce support).

Chapitre 03 Slide 14
Je présente alors le "super algorithme de la dichotomie" (dichotomie, qui vient du Grec "couper en deux"). Et je reprends une partie de la liste dans laquelle Monsieur Jafar vient chercher son prénom (vous ne connaissez pas Monsieur Abu Jafar Muhammad Ibn Musa ? On verra ça un peu plus loin 😉 ).

Chapitre 03 Slide 15
L´algorithme de la dichotomie est très simple. On va voir comment il fonctionne, et on verra plus tard pourquoi il fonctionne. L´algorithme en question dit à Jafar : "regarde si ton prénom est celui du milieu". Jafar s´exécute et le prénom du milieu est... Emilie. De toute évidence, ce n´est pas le sien. Mais il peut faire une chose avec certitude à partir de là. Il peut ... ? Evidemment, l´idée c´est de le faire dire aux participants : il peut enlever tous les prénoms qui sont au-dessus, car le sien est après celui-là.

Chapitre 03 Slide 16
Il vient de se passer quelque chose d´énorme ! Jafar vient d´enlever la moitié du problème ! Et l´algorithme de la dichotomie, d´après vous, lui dit quoi maintenant ? Là encore, l´idée est de le faire dire aux participants... il lui dit de recommencer avec ce qui reste ! Le nouveau problème de Jafar, c´est de trouver son prénom dans la nouvelle liste (diminuée de moitié).

Chapitre 03 Slide 17
Il va donc prendre le nouveau prénom du milieu et... ce n´est toujours pas le sien. Son prénom est avant. Il peut donc... ? Eliminer la moitié inférieure de ce qui reste !

Chapitre 03 Slide 18
Prenons quelques secondes pour regarder ce qui vient de se passer... En deux étapes, on vient d´enlever la moitié du problème, puis encore la moitié de la moitié ! Sur 700 000 prénoms dans la liste du serveur du bac, ça fait beaucoup ! A ce rythme il ne va plus rester grand-chose très rapidement non ?

Chapitre 03 Slide 19
On continue donc et là c´est pas de bol : sur les 4 prénoms on tombe sur le mauvais milieu. Donc on enlève la moitié qui ne correspond pas.

Chapitre 03 Slide 20
je peux donc encore éliminer une partie du problème.

Chapitre 03 Slide 21
Et on recommence... et là c´est gagné !

Chapitre 03 Slide 22
Sur ce coup là, on a mis 4 opérations !

Chapitre 03 Slide 23
On peut montrer facilement que l´algorithme est correct. En enlevant la moitié des prénoms, puis encore la moitié, etc. on voit qu´on arrivera à un seul prénom au final et on pourra dire si le prénom recherché est dans la liste ou pas.

Chapitre 03 Slide 24
: On peut également estimer le nombre d´opérations dans le cas général, c´est à dire préciser la complexité de cet algorithme. Intuitivement, on voit qu´il s´agit de diviser en deux, puis encore en deux, etc., jusqu´à trouver son prénom ou bien affirmer qu´il n´y est pas. Donc combien de fois peut-on couper en deux un ensemble ? J´ai choisi de ne pas écrire la complexité ici. Je préfère la laisser au stade de l´intuition mais, comme pour tout le reste, j´espère qu´un jour on me dira "non c´était mieux de la mettre, d´ailleurs je l´ai fait avec un groupe et..." (bref, ça voudra dire que ce support aura servi à quelqu´un et je ne demande que ça 😉 ! ).

Chapitre 03 Slide 25
Et voilà la conclusion de cette partie, qui me parait le message important (un peu de complexité, mais de manière intuitive). Je peux vous garantir qu´avec un liste de 20 prénoms, la dichotomie mettra 6 opérations, dans le pire des cas, pour répondre à Jafar. Avec une liste de 105 prénoms (comme la liste affichée au début) il lui en faudra 8. Alors d´après vous, avec 700 000 prénoms ... ? J´aime bien inciter les participants à y aller franchement et à faire des essais.

Chapitre 03 Slide 26
Et puis on peut les guider en disant "regardez, de 20 à 105, il y a un gros écart, alors que de 6 à 8...". Ça aide l´intuition. Et bon, on va pas faire durer le suspense toute la nuit : c´est 20 opérations maximum.

Chapitre 03 Slide 27
Ce qui alors intéressant, c´est de comparer ces 20 opérations avec l´algorithme exhaustif. Pour moi, le serveur du bac, je dois toujours répondre à 700 000 requêtes. Mais pour chaque requête, au lieu de 700 000 opérations, je vais en exécuter 20.

Chapitre 03 Slide 28
Je passe donc de 500 milliards d´opérations au total, à 700 000x20 = 14 millions.

Chapitre 03 Slide 29
Alors comparons maintenant les deux approches. D´un côté le super algorithme de la dichotomie, et de l´autre l´algorithme exhaustif. Ils vont donc exécuter respectivement 14 millions d´opérations pour la dichotomie, contre 500 milliards pour l´algorithme qui parcourt toute la liste (du premier au dernier, ou bien au hasard).

Chapitre 03 Slide 30
C´est 35 000 fois plus d´opérations de l´un à l´autre, et une fois l´algorithme implémenté dans une machine, on va très grossièrement estimer que c´est 35 000 fois plus rapide.

Chapitre 03 Slide 31
L´occasion de s´amuser un peu avec les temps de réponse. Si la dichotomie met 1 seconde, alors l´autre mettra 10 heures. Bon, vous me direz "10h pour répondre à tous les candidats du bac en France... c´est pas la fin du monde".

Chapitre 03 Slide 32
Ok, mais si la dichotomie met 1 heure, l´autre en face mettra 4 ans. Là déjà on commence à grincer des dents, et les participants s´en amusent en général ^^ .

Chapitre 03 Slide 33
Si la dichotomie met une journée, alors l´autre mettra 96 ans ! ! Bon... alors 96 ans pour savoir si tu as le bac... peut-être que tu as d´autres préoccupations depuis...

Chapitre 03 Slide 34
et là c´est pour voir si vous êtes réveillés 😀 . Si la dichotomie met 1 an ? L´autre mettra... ? Bah 35 000 ans puisqu´il est 35 000 fois plus rapide 😉 !Donc, en fonction de l´algorithme qu´elle utilise, une même machine sera plus ou moins rapide pour résoudre un problème.