Projet (EPI) « Synthétiseur » – Séance 2 Le timbre et les harmoniques

1, 2, 3, codez ! - Activités cycle 4 - Projet (EPI) « Synthétiseur » - Séance 2 : Le timbre et les harmoniques
|
Discipline dominante |
Physique-chimie |
|
Résumé |
Les élèves découvrent le timbre de sons artificiels. Parmi eux, le signal sinusoïdal ressemble fortement au son du diapason : les élèves s’intéressent alors à la décomposition fréquentielle du timbre de divers instruments. |
|
Notions |
Information
Machines
|
|
Matériel |
Pour la classe :
Par binôme :
|
Préparation de la séance
Avant la séance, l’enseignant génère des sons de fréquence donnée
(440Hz) mais de formes différentes : sinusoïdale, carrée,
dents-de-scie…
Pour cela, il existe de nombreux outils :
- générateur électromécanique : un générateur de fonctions alimentant un haut-parleur ;
- générateurs sur tablette ou smartphone :
- https://itunes.apple.com/app/id903272957
- https://itunes.apple.com/us/app/sgenerator-lite/id545708475?mt=8
- logiciel Audacity : dans le menu Générer > Son, on peut créer des sons artificiels avec une forme d’onde, une fréquence et une amplitude bien déterminées. Dans ce cas précis, laisser les valeurs par défaut de fréquence (440 Hz) et d’amplitude (0,80).
Situation déclenchante
Au cours de la séance précédente, les élèves ont observé les
différentes formes d’onde des sons produits par différents instruments.
L’enseignant leur fait écouter les signaux artificiels qu’il a générés
avant la séance. Les élèves remarquent que les timbres de ces sons sont
tous différents (et, en général, peu agréables à l’oreille).
L’enseignant zoome sur l’échelle des temps pour observer la forme du
signal. Les élèves peuvent ainsi se remémorer expérimentalement que le
timbre est lié à la forme du signal.
Le professeur projette les enveloppes3 mesurées pour les La3 des
différents instruments vus en Séance 1 (expérience III). Toutes ces
ondes sonores ont la même fréquence (si la même note a pu être jouée par
tous les instruments), donc la même période. Selon l’enregistrement,
l’amplitude varie, mais le professeur insiste sur les variations de la
forme de l’onde. En particulier, le diapason a un son de forme bien
sinusoïdale.
Le professeur demande alors : comment différencier le signal du diapason d’une sinusoïde artificielle ?
Observation : timbres et harmoniques (en classe entière)
Au tableau, il projette sa propre fenêtre Audacity. Il enregistre (ou charge) quatre pistes simultanément : deux pistes avec le son d’un diapason La3 et deux pistes avec le son artificiel à 440Hz. En zoomant à l’échelle du centième de seconde, on peut voir une belle sinusoïde : le son du diapason est presque pur, ce qui fait de ce dernier un excellent étalon sonore. Mais l’enseignant dévoile un nouvel outil : l’analyse spectrale.
- Lorsqu’il clique sur l’onglet Piste Audio > Spectrogramme, la visualisation du son change complètement.
- Lorsqu’il clique sur l’onglet Piste Audio > Forme d’onde, on revient à la visualisation précédente.
Il affiche donc quatre graphes différents simultanément : la forme d’onde du diapason, le spectrogramme du diapason, la forme d’onde de la sinusoïde, le spectrogramme de la sinusoïde.
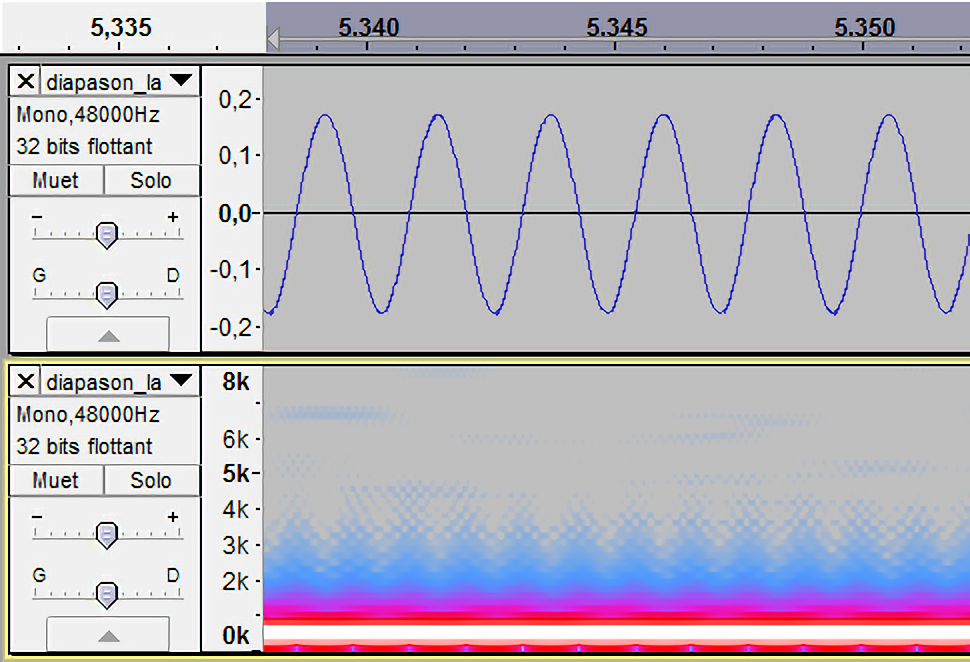
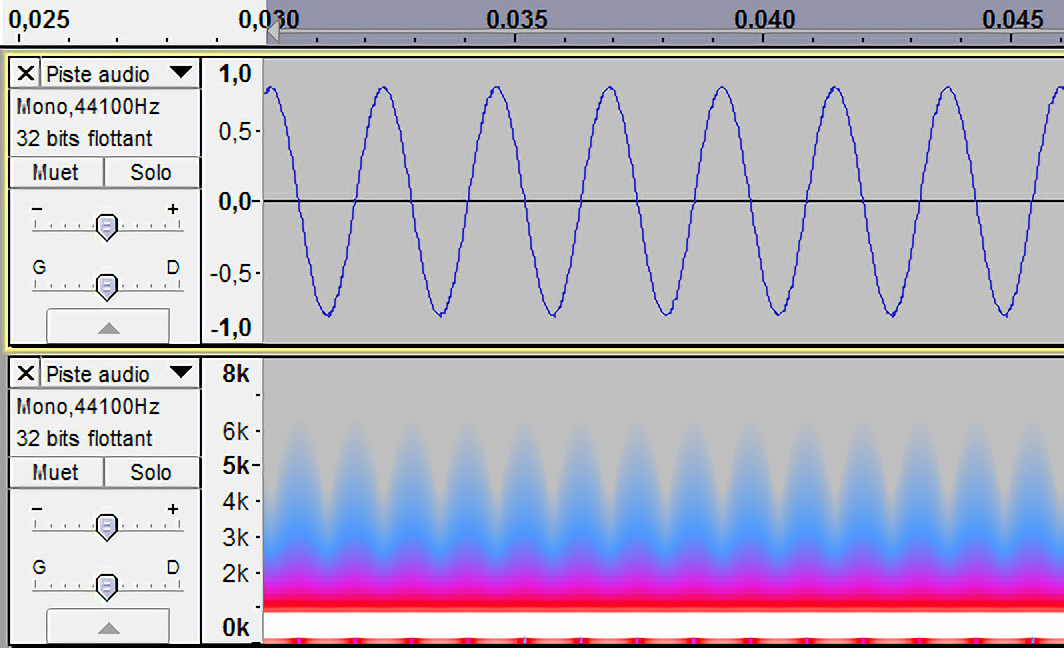
Diapason La3 (440 Hz) à gauche, sinusoïde 440Hz à droite.
Forme d’onde en haut, spectrogramme en bas.
L’enseignant explicite ce nouveau graphe : en abscisse se trouve le temps, et en ordonnée sont classées des fréquences. La couleur code l’intensité relative de chaque fréquence sonore à chaque intervalle de temps (blanc pour les plus intenses, puis rouge, rose, et bleu pour les plus faibles).
Note pédagogique :
- L’analyse spectrale présentée ici s’appelle Transformée de Fourier. Ce terme est bien évidemment hors programme de l’enseignement secondaire. Au cycle 4, on peut se contenter de dire qu’un spectrogramme permet de visualiser la répartition des différentes fréquences qui composent une onde en fonction du temps.
- La compréhension attendue de cet outil est minimaliste : il doit permettre aux élèves de repérer facilement la simplicité ou la complexité d’un son (ou en termes plus imagés, la pureté ou la richesse de ce son).
Si l’on observe le spectre du diapason, on voit principalement une
grande barre blanche horizontale, et un tout petit peu de bruit
alentours. Voilà comment on peut différencier le signal du diapason réel
de la sinusoïde générée artificiellement.
Chaque groupe doit maintenant effectuer la même manipulation sur son
propre échantillon. Simultanément, l’enseignant fait de même avec
l’échantillon de flûte qui avait été enregistré en classe entière.
Dans le cas des instruments autres que le diapason, on voit plusieurs
bandes blanches, ainsi que d’autres rouges ou roses. Les élèves
observent que les sons les plus complexes, dont la forme d’onde était
très éloignée de la sinusoïde, ont un spectrogramme très fourni. La
corde de guitare donne un son assez simple, alors que celui du violon
est très compliqué.
La fréquence la plus intense est appelée fondamentale ; les fréquences secondaires sont appelées harmoniques.
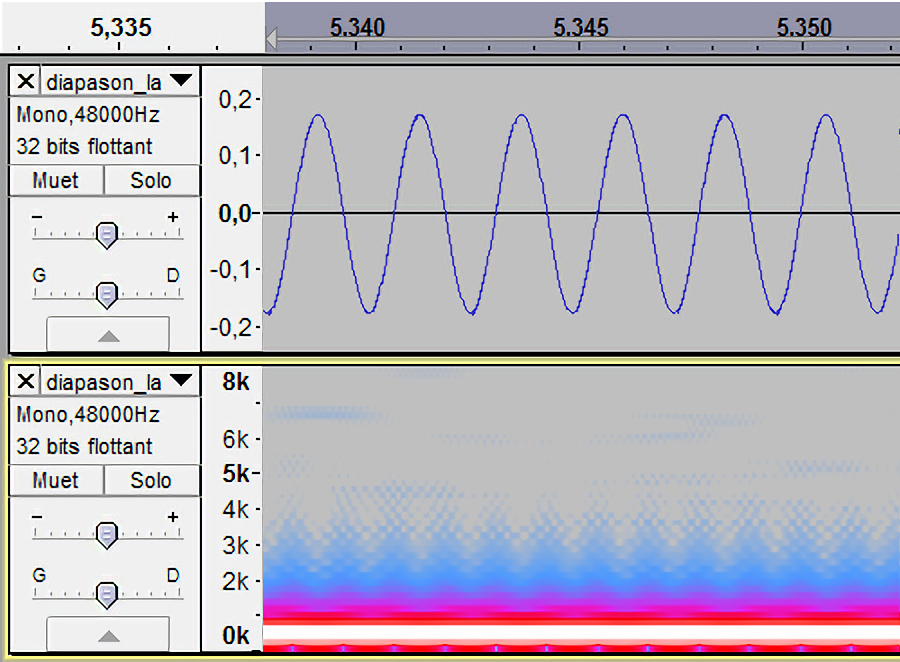 Le diapason |
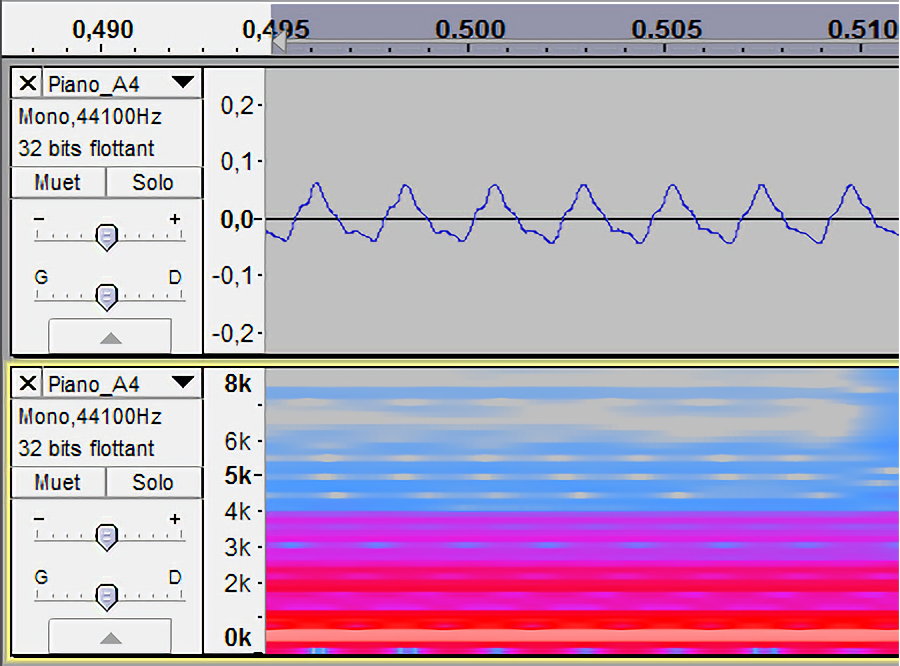 Le piano |
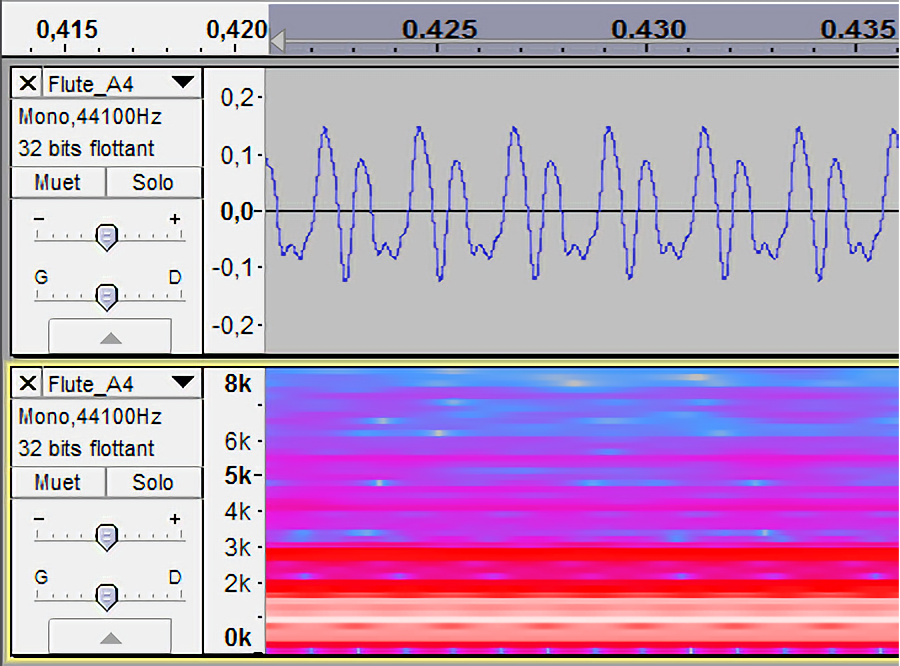 La flute |
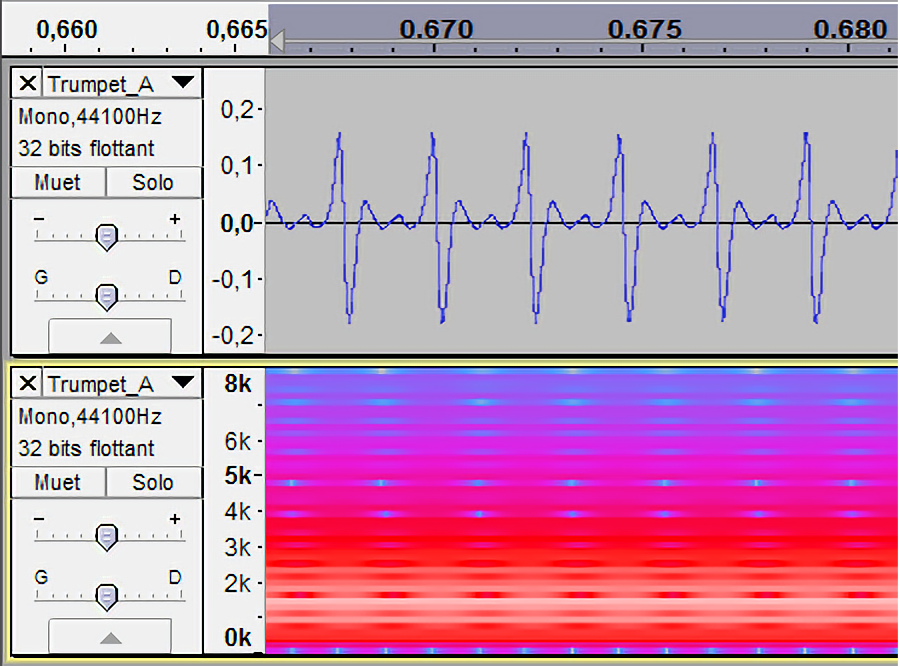 La trompette |
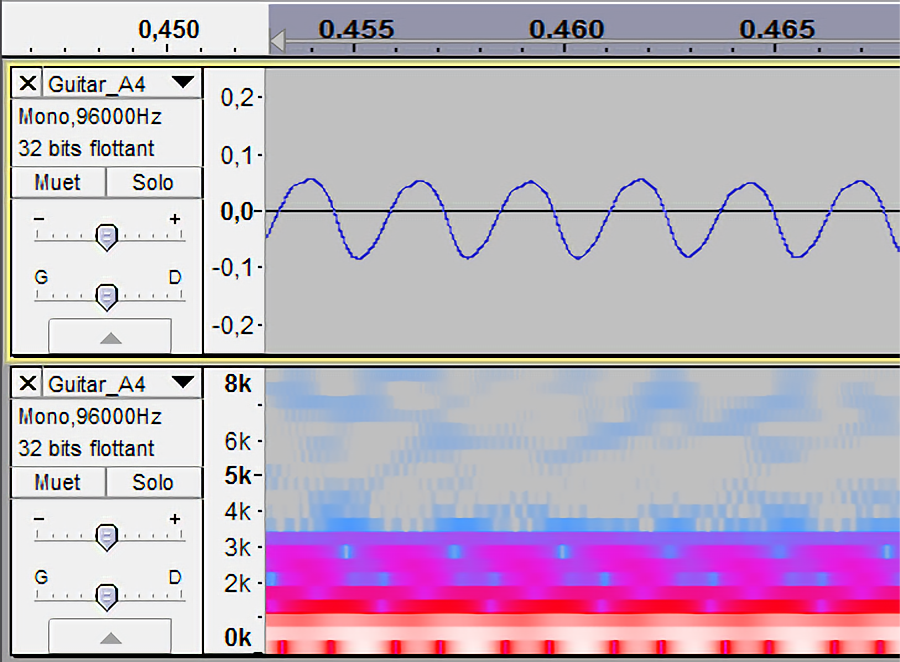 La guitare |
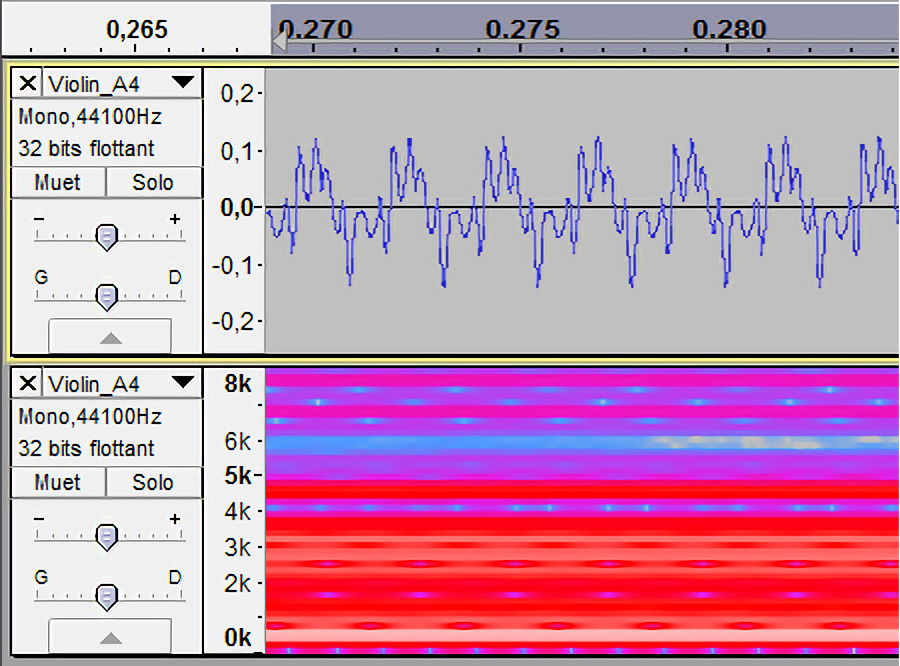 Le violon |
Notes scientifiques :
- Nous définissons ici les harmoniques comme des multiples (entiers ou fractionnels) d’une fréquence fondamentale (voir note scientifique ci-après). Avec Audacity, il est possible d’identifier la fréquence de ces harmoniques, mais cela nécessite un outil supplémentaire (permettant de visualiser le spectre du signal). Nous proposons cette activité dans la séance optionnelle 7 : nous nous limitons ici à une expérience plus simple.
- Par définition, la fondamentale est la fréquence propre de vibration de l’émetteur sonore. Une harmonique est alors un multiple entier (exclusivement) de cette fondamentale.
Lorsque l’on étudie la Transformée de
Fourier d’un son, la fondamentale peut très bien ne pas être
visible : il s’agit du plus petit commun diviseur de toutes les
harmoniques mesurées. Par exemple, le spectre du La3 à la guitare montre
un pic principal à 440Hz et un pic secondaire à 220Hz : la note
ressentie est bien un La3, mais la fondamentale est 220Hz et le La3 n’en
est que la première harmonique. De surcroît, la structure physique même
de l’instrument peut autoriser des partiels : des fréquences
émises par l’instrument qui ne sont pas des harmoniques (des multiples
non entiers de la fondamentale, en quelque sorte des « harmoniques
inharmoniques », qui ne sont pas en « harmonie » avec la
fondamentale).
Dans ces conditions, nous préférons fournir une définition légèrement
faussée de « fondamentale » et « harmonique » (en
repérant le pic principal et en autorisant les multiples fractionnels)
qui sera plus facile d’utilisation auprès des élèves.
Observation : écoutons des harmoniques (en classe entière)
Pour mieux décrire les harmoniques, l’enseignant propose aux élèves d’utiliser à nouveau les générateurs de son d’Audacity.
Dans un premier temps, les élèves génèrent une fondamentale sinusoïdale
à 440Hz (amplitude par défaut 0,80). Puis ils ajoutent une seconde
piste (Pistes > Ajouter une nouvelle > Piste mono ou
Ctrl+Shift+N) sur laquelle ils génèrent un autre son, sinusoïdal lui
aussi, d’amplitude moindre (0,40), mais de fréquence 880Hz. Lorsqu’ils
écoutent simultanément les deux sons, ils constatent que
l’impression sonore a changé, même si l’on reconnaît bien le La initial.
Dans un second temps, les élèves créent une troisième piste : ils
la peuplent d’une sinusoïde à une fréquence proche mais différente de
880Hz, par exemple 860Hz (amplitude 0,40). Avant d’écouter le résultat,
ils rendent muette (bouton « Muet » sur la colonne de gauche)
la piste 2. Le son est plus nasillard, moins harmonieux (les oreilles
des mélomanes en seront parfois douloureuses selon l’appariement
aléatoire choisi) : on retrouve l’étymologie du terme
« harmonique ».
L’enseignant complète alors la définition de « fréquence
harmonique » : une fréquence multiple d’une fréquence
fondamentale.
Les élèves peuvent regarder d’autres spectrogrammes d’autres
instruments, ou d’autres générateurs (fonctions carrée, en dents de
scie, etc.), combiner des harmoniques avec des facteurs autres que 2…
Conclusion
La classe élabore une conclusion commune qui sera écrite dans les cahiers de projet :
- Le timbre est spécifique à un instrument : il est produit par une combinaison d'harmoniques.
- La combinaison de certaines fréquences peut être harmonieuse ou discordante à l’oreille.
Variante électromécanique
Si la classe ne dispose pas d’ordinateurs, ou pour compléter la
séance, il est possible d’étudier les harmoniques avec un oscilloscope.
Il est par exemple possible d’utiliser un premier générateur de
fonctions basse fréquence pour alimenter un haut-parleur : le
générateur BF permet souvent de choisir la forme du signal (sinusoïdal,
carré, triangulaire, etc.). À fréquence et amplitude fixées, le son produit change selon la forme du signal. C’est la signature du timbre.
Un microphone branché sur l’oscilloscope permet de visualiser en sortie la forme de l’onde émise.
On peut également, dans un second temps, combiner les signaux de deux
générateurs BF : en mixant deux sinusoïdes de fréquences et
amplitudes différentes, on peut générer une nouvelle onde de forme
complexe, dont le timbre est particulier (attention aux mélomanes :
des fréquences aléatoires sont souvent dissonantes et très désagréables
à l’oreille). Sur l’oscilloscope de sortie, l’onde résultante n’a plus
rien de sinusoïdal (il suffit d’arrêter l’un des deux générateurs pour
retrouver immédiatement un son pur et une onde sinusoïdale).
On parle donc de fréquence fondamentale pour l’onde ayant la plus grande amplitude.
Si la fréquence de la deuxième onde est un multiple de cette
fréquence fondamentale, le son produit par la combinaison de ces 2 ondes
devient plus harmonieux : on parle alors d’harmonique.
Extrait de "1, 2, 3... codez !", Editions Le Pommier, 2016-2017. Publié sous licence CC by-nc-nd 3.0.
