Avant-propos

Cette séance est conçue pour être co-animée par les professeurs de musique et de mathématiques. Le professeur de musique pourra aider les groupes à coucher sur le papier leur partition et à rappeler les règles d’écriture, tandis que le professeur de mathématiques proposera une analyse de la représentation de l’information : l’écriture musicale est un langage spécialisé, distinct à plus d’un titre de la langue naturelle.

Note pédagogique :
 L’étude de l’écriture musicale par les mathématiques peut se faire de deux façons :

•  La notation musicale est un encodage d’information (ce que nous faisons ici) ;
•  On peut lier l’étude de la représentation graphique de la musique et la géométrie (ce que nous proposons en prolongement de cette séance).

Situation déclenchante

Pour le mode automatique de leur futur synthétiseur, les élèves devront introduire des mélodies prédéfinies. Ils ont certainement une petite idée de la musique qu’ils voudraient faire jouer à Scratch. Ils vont décider au cours de cette séance la mélodie définitive. Pour cela, le professeur de musique doit les aider à en établir la partition.
Cela nécessitera probablement de simplifier la mélodie (un seul instrument) et ses arrangements. Si la classe manque de temps, aiguiller les élèves vers une mélodie pentatonique (qui ne nécessitera la programmation que de 5 lutins musiciens). Si la classe veut faire jouer les programmes des différents groupes de concert, prévoir des mélodies compatibles entre elles…
Quand la mélodie est choisie, il reste à en écrire la partition.

Éclairage historique : les gammes et les partitions (classe entière, 10 minutes)

Si la classe n’en est pas à sa première leçon de formation musicale (solfège), les élèves auront déjà des notions : partitions, notes, accords… Notions déjà survolées rapidement lors du brainstorming lexical de la Séance 1.
C’est l’occasion de donner un rapide éclairage historico-scientifique sur les gammes pentatonique, pythagoricienne, tempérée…  Par goût ou par limitation technique, chaque culture a pu faire des choix sur les sons jugés « harmonieux », et créer des normes en conséquence, appelées « gammes ». Si la classe est cosmopolite (avec de grandes probabilités qu’un groupe choisisse une musique orientale, les musiques d’Orient et d’Extrême Orient étant souvent basées sur des gammes pentatoniques.), ou si la classe est à court de temps, l’enseignant peut insister particulièrement sur la gamme pentatonique.

Note scientifique :

•  C’est au XIe s que Guy d’Arezzo a posé les prémices des partitions modernes, en cherchant à codifier la notation musicale. En particulier, il renomme les notes, initialement décrites par les premières lettres de l’alphabet (notation conservée par les pays anglo-saxons), par un acrostiche dédié à saint Jean-Baptiste :

 Note : le B anglophone correspond au sib. Depuis le XVIe s, UT a été renommé DO, car l’acrostiche pouvait être précédée de l’invocation Domine (ô Seigneur).

•  La définition de « gamme » est multiple : cela peut décrire la collection de notes utilisables (do, ré, mi, etc. ; c’est ce sens que nous utilisons dans cette séance) ; cela peut aussi décrire la répartition des notes les unes par rapport aux autres (ce qu’on appelle aussi « tempérament », qui sera étudié en Séance 6) ; enfin, c’est un type d’exercice de dextérité (« faire ses gammes »).

Le professeur pose alors la question : un instrument peut-il jouer d’autres notes que celles de la gamme en vigueur ?

Observation : comparer des instruments à cordes

L’enseignant montre alors un violon et une guitare. Les deux instruments se ressemblent beaucoup, et encore plus si le violon est joué en pizzicato.
Maintenant, l’enseignant joue quelques notes sur une corde donnée, en variant progressivement la position de ses doigts. Les élèves peuvent s’aider d’un accordeur pour relever les différentes fréquences jouées. La question est simple : comment se répartissent les fréquences des notes jouées ?
Les élèves remarquent vite une différence dans la succession des notes :

•  Le violon est un instrument à son continu : on peut faire varier progressivement et continument les notes.
•  La guitare est un instrument à son fixe : à cause des frettes, la corde ne peut vibrer qu’à certaines fréquences données, et pas à d’autres (aux bends près, que nous omettrons ici).

Cette observation confirme que des choix esthétiques ou culturels ont été effectués, comme cela a été vu plus tôt dans la séance : les accords, les gammes et les partitions sont construits pour n’autoriser que des sons qui « vont bien ensemble ».
Les élèves écrivent une conclusion similaire dans leur cahier de projet :

•  Une gamme est définie pour ne permettre de jouer que des sons harmonieux.

Application : écrivons nos partitions (collectivement)

Les élèves peuvent retranscrire la mélodie qu’ils ont choisie, collectivement, avec l’aide du professeur de musique. Celui-ci leur demande quelles sont les conventions de l’écriture musicale. S’ils ont déjà eu au moins un cours de formation musicale, les réponses fusent rapidement :

•  la position verticale sur la portée représente la hauteur (fréquence) de la note, aux altérations près (+/- 1/2 ton) ;
•  la couleur/forme représente la durée de la note ;
•  la succession de gauche à droite représente l'écoulement du temps.

L’enseignant peut proposer de petits exercices de lecture/écriture : lire des partitions simples et les jouer, retranscrire des mélodies simples. Le but ici est d’explorer la variété des possibles : des clefs de Sol ou de Fa, des rythmes lents ou rapides, etc.

Observation : l’écriture musicale est un langage (classe entière)

Le professeur de mathématique affiche au tableau la Fiche 1 qui avait servi au brainstorming du lexique musical en Séance 1. En particulier, il demande aux élèves quelles sont les valeurs précises que peuvent prendre les notions qu’ils ont listées plus haut : hauteur, durée, rythme.

Les élèves énumèrent :

•  La hauteur (la fréquence) de la note est définie sur la portée : soit sur un des traits, soit entre deux traits, il n’existe pas d’alternative. Les notes altérées sont signalées par un # ou un b. La clef permet de donner une origine à l’échelle verticale.
•  La durée de la note : ronde, blanche, noire, croche, pointée ou non. Même les silences sont indiqués et temporisés.
•  Le tempo est donné par une indication proche du titre de la partition.
•  Le volume (la nuance) peut être indiqué par des indicateurs de nuance tels que f(forte) ou p(piano), tandis que les changements progressifs de nuance peuvent être repérés par  des signes croissants ou décroissants au-dessus de la portée.
•  Le temps est étalonné par mesures.
•  Le timbre est partiellement défini car il est possible d’indiquer un instrument préférentiel par portée.

Le professeur de mathématique explicite alors que l’écriture musicale est un langage. Un langage très spécialisé, dont le vocabulaire est très restreint (une vingtaine de caractères énumérés plus haut), et dont la syntaxe est très simple (les signes sont écrits de gauche à droite, dans leur succession chronologique ; une mesure ne peut contenir qu’un certain nombre de temps, ni plus ni moins). L’information qui a été encodée sur cette partition peut être décodée à l’identique.

Note scientifique:
 Le langage musical partage quelques propriétés communes avec les langages de programmation, mais il n’en est pas réellement un. D’une part, il laisse libre cours au talent d’interprétation du musicien qui peut s’éloigner un peu de la partition écrite. De même, il n’est pas très robuste aux erreurs : il y a mille façons de corriger une erreur dans une partition, laissées à la discrétion du musicien.

Avec l’aide du professeur de musique, le professeur de mathématique demande aux élèves si l’information encodée dans une partition est sensible aux erreurs, et si elle y est robuste. Que se passerait-il si on se trompait en recopiant la partition ?

•  Si on se trompe de couleur sur une note, peut-on repérer qu’il y a une erreur ? Oui : le nombre de temps dans la mesure est erroné. Peut-on la corriger ? Non, ce sera au musicien d’imaginer quelles notes pourraient esthétiquement se trouver là.
•  Si on se trompe de hauteur, est-ce grave ? La musique est modifiée, et il n’est pas possible, a priori, de détecter et corriger cette erreur[d15]. Cependant, les musiciens travaillent souvent en suivant des accords et des arpèges précis, ce qui rend parfois possible de détecter une telle erreur (à condition que le compositeur n’ait pas choisi, sciemment, de créer un petit déséquilibre afin d’éviter une mélodie trop scolaire).
•  Si on se trompe de tempo ? Ce sera au musicien d’interpréter selon son goût et sa culture des habitudes du compositeur…
•  Etc.

Exercices : le langage MIDI (par groupes)

Lorsque les groupes ont achevé l’écriture de leur partition, le professeur de mathématiques leur propose de la traduire dans un nouveau langage. Comment pourriez-vous décrire la partition à un ordinateur ? Si les élèves n’ont pas d’idées, l’enseignant leur rappelle qu’en Séance 1, ils avaient émis l’hypothèse que l’enregistreur du synthétiseur avait « enregistré la succession des pressions sur les touches ».
Les élèves vont proposer un langage qui pourrait ressembler à ceci : « joue un La pendant 1 seconde, joue un Sol pendant 3 secondes, fait un silence pendant 1 seconde… ».

Le professeur leur annonce qu’ils viennent de découvrir par eux-mêmes le principe du langage MIDI (Musical Instrument Digital Interface), inventé dans les années 1980, pour transmettre une partition à un instrument électronique. C’est exactement comme cela que fonctionne l’enregistreur du synthétiseur. Dans l’optique de pouvoir faire jouer leur partition par un programme sous Scratch, les élèves vont devoir s’entraîner à passer du langage musical au langage MIDI.
 

Note pédagogique:
 Il n’est ni utile ni pertinent de vouloir apprendre ici la syntaxe réelle du langage MIDI (voir par exemple à ce sujet les sites internet www.jchr.be/linux/format-midi.htm ou www.music.mcgill.ca/~ich/classes/mumt306/StandardMIDIfileformat.html). La seule compréhension de son principe suffit amplement.

Avant que les élèves ne se lancent dans la traduction de leur propre mélodie, les deux professeurs proposent quelques exercices préliminaires : ils distribuent alors la Fiche 4.

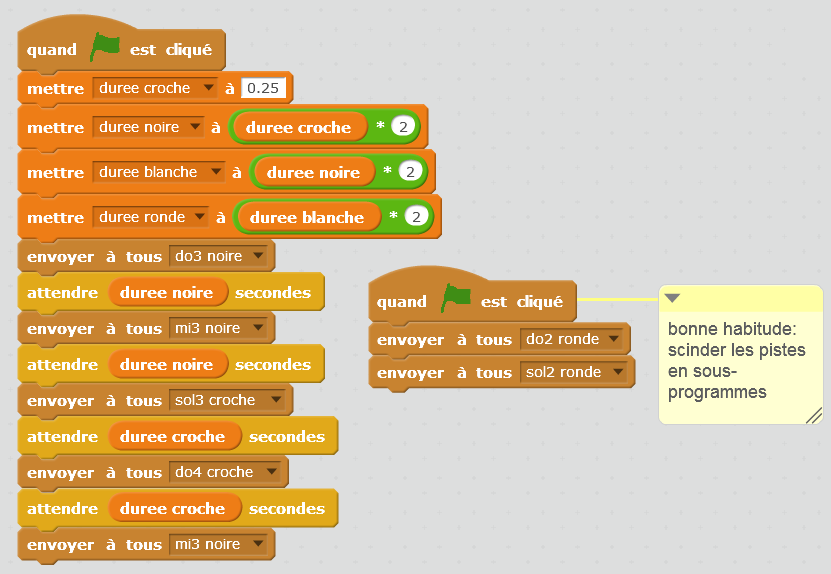
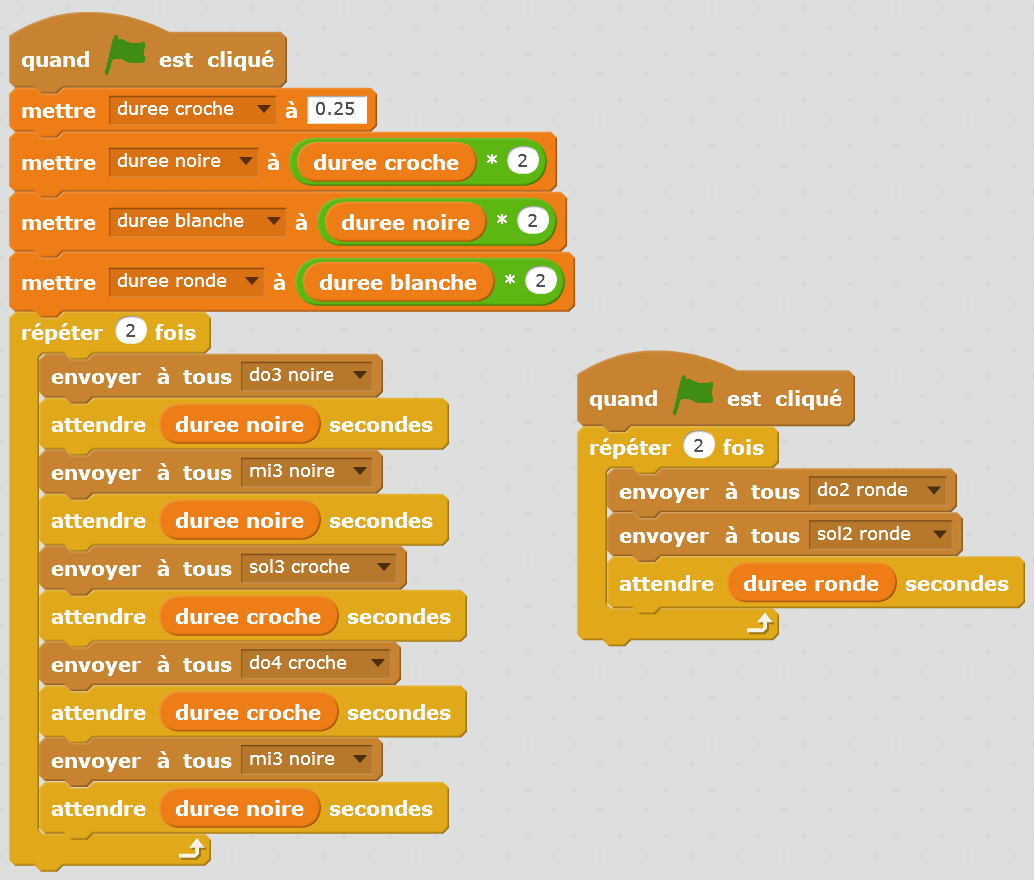
Nous proposons ici quatre exercices, ainsi que leur corrigé sous  forme de logigrammes ainsi que leur traduction en langage Scratch (la programmation Scratch sera réalisée en Séance 5 : les programmes sont donnés à titre d’information pour le professeur et n’ont pas besoin d’être montrés aux élèves à ce stade, sauf évidemment s’ils connaissent déjà Scratch). Ces exercices peuvent se diversifier à l’infini, mais ces exemples permettent de voir des arpèges, des accords et des boucles.

Partition 1
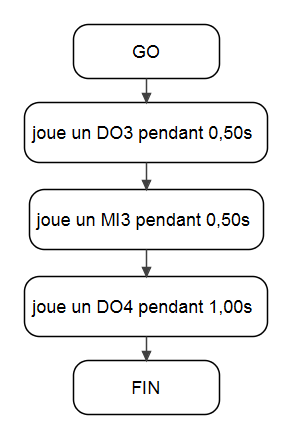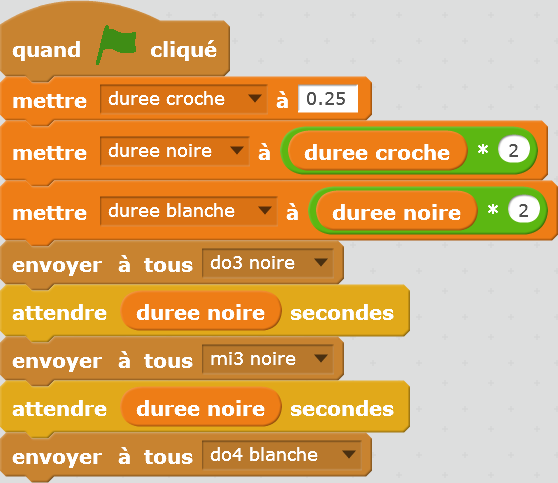Partition 2
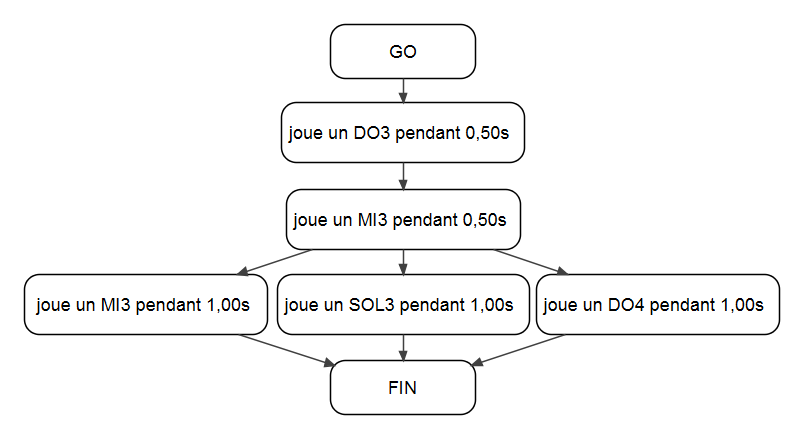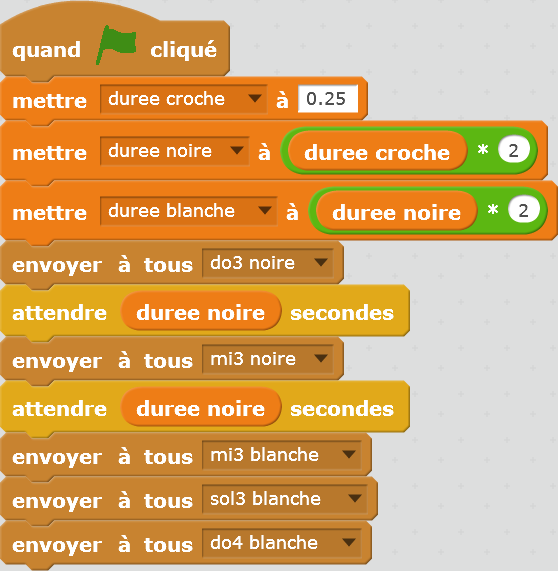Partition 3
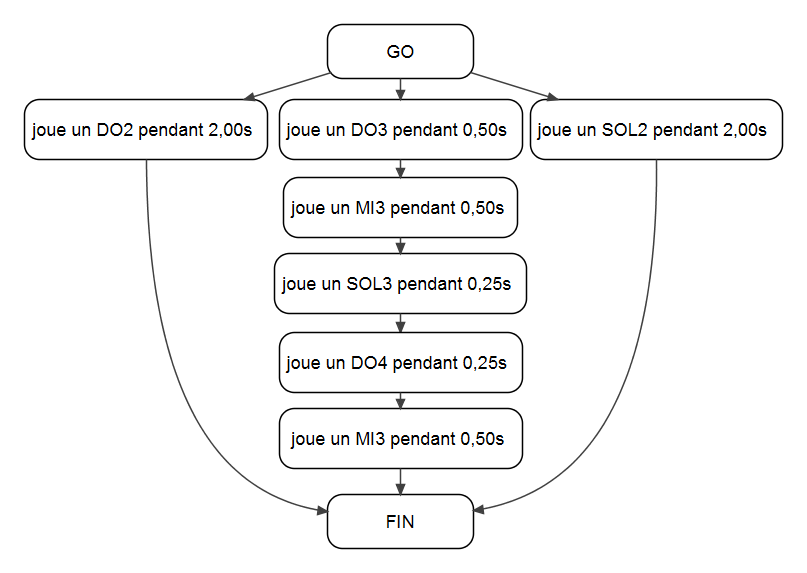Partition 4

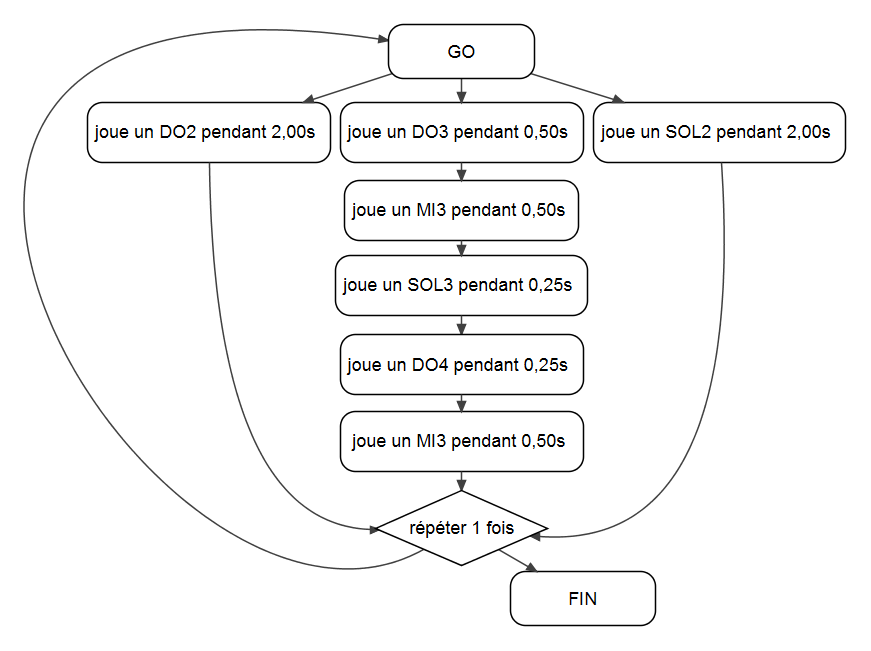Conclusion

Dans leur cahier de projet, les élèves ajoutent une conclusion du type :

•  L’écriture musicale est un langage permettant d’encoder de l’information.
•  Le langage MIDI encode la partition pour qu’un ordinateur puisse la jouer.
•  On peut passer d’un langage à l’autre.

Prolongement : encoder la partition sous forme de séquence temporelle (par groupes)

Les enseignants distribuent aux groupes des partitions perforées pour boîte à musique configurable [Qu’on peut trouver, par exemple, ici : http://www.amazon.fr/Bo%C3%AEte-Musique-Faire-Soi-M%C3%AAme-Kikkerland/dp/B00D475PBA , ou http://www.scienceshopping.com/boite-a-musique-avec-papier-a-perforer.html], mais sans distribuer les boîtes à musique ! Les élèves doivent tenter de deviner la mélodie.
Cet exercice permet de réaliser que la partition a été légèrement modifiée : on peut certes la lire grâce aux repères de la carte perforée, mais une information a disparu : toutes les notes semblent avoir la même durée. Ce « blanc » entre deux notes correspond-il à un silence ou à une note longue mal encodée ? Une partie de l’information a disparu lors de l’encodage, à cause des limitations techniques. Cet encodage n’est pas bijectif.

Dans un second temps, les enseignants distribuent les boîtes à musique. Les élèves peuvent vérifier leur interprétation. Ils découvrent à ce moment une autre ambiguïté de cet encodage : c’est la vitesse de défilement de la carte perforée qui représente le tempo, mais il n’y a aucune indication sur la vitesse à adopter.

Enfin, des cartes vierges sont distribuées pour que les groupes puissent s’entraîner à encoder leur propre partition.

Note scientifique
 Cette activité est une belle occasion de parler un peu plus du ruban perforé et de son rôle dans l'histoire de l'informatique : représenter une information sur un support concret (le ruban) et permettre sa lecture par une machine. Ici, le ruban permet d’encoder un signal sonore. Mais le même principe (ruban ou carte perforée) a aussi permis, historiquement, de représenter des images (sur une étoffe, via le métier à tisser de Jacquard), puis un programme enregistré et ses données, d'abord dans une version conceptuelle (la machine universelle de Turing) puis dans des versions concrètes (premiers calculateurs électro-mécaniques : Zuse 3, premiers ordinateurs : ENIAC…).
 La carte perforée a été peu à peu remplacée, d’abord par des supports magnétiques (bandes, puis disques durs), puis par des supports optiques (CD, DVD) ou électroniques (mémoires flash).

Prolongements

Histoire de l’écriture musicale (éducation musicale)

Une recherche bibliographique peut être menée pour étudier l’évolution de la notation musicale :

•  les accords mélodiques notés à même le texte sur les odes grecques du VIe s v. J-C ;
•  les neumes du chant grégorien (IXe s) ;
•  les notes, les portées et les clefs de Guido d’Arezzo (XIe s) ;
•  l’apparition des polyphonies au XIIe s ;
•  les imitations de la Renaissance ;
•  Le clavier bien tempéré de J.S. Bach…

Cette recherche peut être inspirée par la présentation de partitions antiques lors de l’étude de cas proposée plus haut.

Musique et géométrie (mathématiques)

On peut facilement faire des parallèles entre certaines figures de style musicales et des transformations géométriques du programme :

•  Le canon est une partition jouée par un second instrument, identique à la première, mais décalée dans le temps ; c’est une translation selon l’axe du temps.
•  La transposition est un décalage d’un ou plusieurs demi-tons ; cela correspond à la multiplication par un même facteur des fréquences de toutes les notes : sur la portée (qui est une représentation logarithmique !) cela se traduit par une translation sur l’axe vertical.
•  Le contrepoint est une partition miroir de la première (si la mélodie primaire monte d’une tierce, alors son contrepoint descend d’une tierce) ; c’est une symétrie verticale.
•  L’imitation en écrevisse joue la partition primaire en remontant l’axe du temps ; c’est une symétrie horizontale.