Projet « Cryptographie » – Séance 4 Casser le chiffrement mono-alphabétique

1, 2, 3, codez ! - Activités cycle 4 - Projet « Cryptographie » - Séance 4 : Casser le chiffrement mono-alphabétique
|
Discipline dominante |
Mathématiques |
|
Résumé |
Les élèves découvrent et appliquent la méthode d’analyse fréquentielle inventée par Al-Kindi, nécessitant des allers-retours entre la statistique et la linguistique. |
|
Notions |
« Information »
|
|
Matériel |
Pour la classe
Pour chaque élève |
Situation déclenchante
Le professeur revient sur ce qui a été vu lors de la séance
précédente : en raison du très grand nombre de clés possibles, le
chiffrement par substitution mono-alphabétique semble incassable. En
effet, essayer toutes les clés prendrait des milliers d’années (avec un
supercalculateur)… ou des milliards d’années (à la main).
Il annonce pourtant que ce chiffrement n’est plus utilisé depuis le
Moyen-Âge, car un savant perse a trouvé une méthode permettant de
trouver la clé rapidement (Al-Kindi, 9è siècle après J.-C.).
Le professeur demande à la classe comment Al-Kindi a bien pu s’y
prendre. S’ils n’ont aucune idée, il les guide en leur demandant
d’expliquer comment ils avaient « cassé » le chiffrement de
César (cf. Séance 2).
Outre la possibilité d’essayer toutes les clés possibles, la classe
avait repéré quelle était la lettre la plus fréquente dans la langue
française (le « E »), puis elle avait fait l’hypothèse que
toutes les lettres avaient subi le même décalage que le « E ».
Cette hypothèse n’est plus justifiée dans le cadre d’un chiffrement
mono-alphabétique quelconque : chaque lettre peut, a priori,
correspondre à n’importe quelle autre. Il faut donc s’aider de plusieurs
lettres fréquentes, et pas d’une seule.
Trouver les lettres les plus fréquentes en français (collectivement, puis par binôme)
Le professeur demande si les élèves savent quelles sont les lettres les plus fréquentes en français et, dans le cas contraire, comment ils pourraient le déterminer.
Une première manière d’approcher le problème consiste à examiner un jeu de Scrabble. Les lettres possèdent chacune une valeur et, bien entendu, les lettres les plus rares rapportent le plus de points (il est plus difficile de placer un W qu’un E dans un mot français !). Par ailleurs, on remarque que les lettres qui rapportent le moins de points (donc, a priori, les plus fréquentes), sont présentes en de nombreux exemplaires dans le jeu.
|
Lettre au Scrabble© |
A1 |
B3 |
C3 |
D2 |
E1 |
F4 |
G2 |
H4 |
I1 |
J8 |
K10 |
L1 |
M2 |
N1 |
O1 |
P3 |
Q8 |
R1 |
S1 |
T1 |
U1 |
V4 |
W10 |
X10 |
Y10 |
Z10 |
|
Nombre d’exemplaires de chaque lettre. |
9 |
2 |
2 |
3 |
15 |
2 |
2 |
2 |
8 |
1 |
1 |
5 |
3 |
6 |
6 |
2 |
1 |
6 |
6 |
6 |
6 |
2 |
1 |
1 |
1 |
1 |
Après avoir fait examiner les pièces par les élèves, il affiche la répartition des lettres au tableau et demande aux élèves, par binôme, de créer un histogramme.
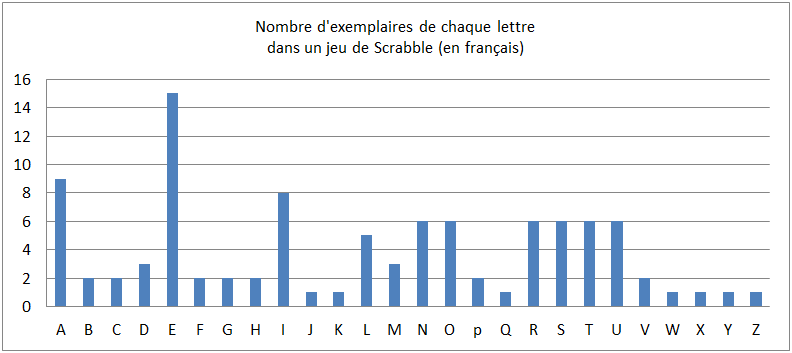
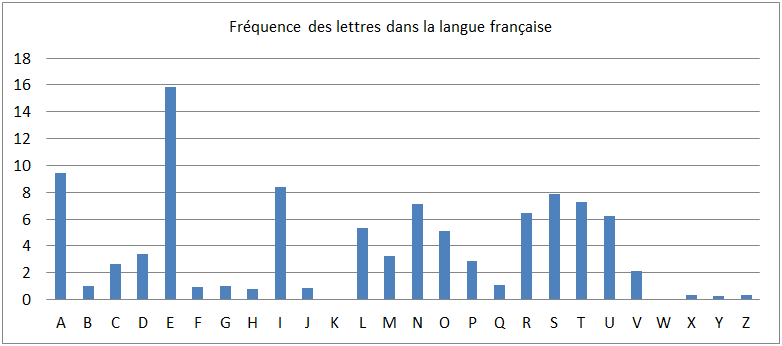
Cet histogramme est très proche de celui obtenu pour la langue française en général :
Note scientifique
- Il n’est pas possible de donner un histogramme de référence unique pour une langue donnée, quelle qu’elle soit, car les lettres les plus fréquemment employées dépendent du type de texte et du registre d’écriture (télégramme diplomatique, œuvre littéraire, encyclopédie, langage familier…). Cependant, les différences d’un registre à l’autre peuvent être négligées dans un tel projet pédagogique.
- Les histogrammes de référence figurant sur la Fiche 7 ont été produits en analysant de grands corpus de texte (dictionnaires, œuvres littéraires…) [Source : en.wikipedia.org/wiki/Letter_frequency ]. Nous les avons modifiés pour tenir compte de notre alphabet simplifié (les statistiques pour la lettre « e » regroupent également celles des lettres « é », « è », « ê »…).
Mise en commun
Après avoir corrigé les productions des élèves, le professeur demande
à la classe si cette fréquence constatée pour le Scrabble reflète la
fréquence des lettres de la langue française. Il propose, pour le
savoir, d’analyser un texte figurant dans l’exercice 1 de la Fiche 6 (il s’agit du préambule à la Déclaration universelle des droits de l’homme et du citoyen de 1789).
Pour gagner du temps, chaque élève ne travaille que sur 2 ou 3
lettres seulement (ce qui permet, malgré tout, de comparer les
productions de plusieurs élèves pour une même lettre et ainsi de
détecter d’éventuelles erreurs).
Finalement, un histogramme est produit collectivement :
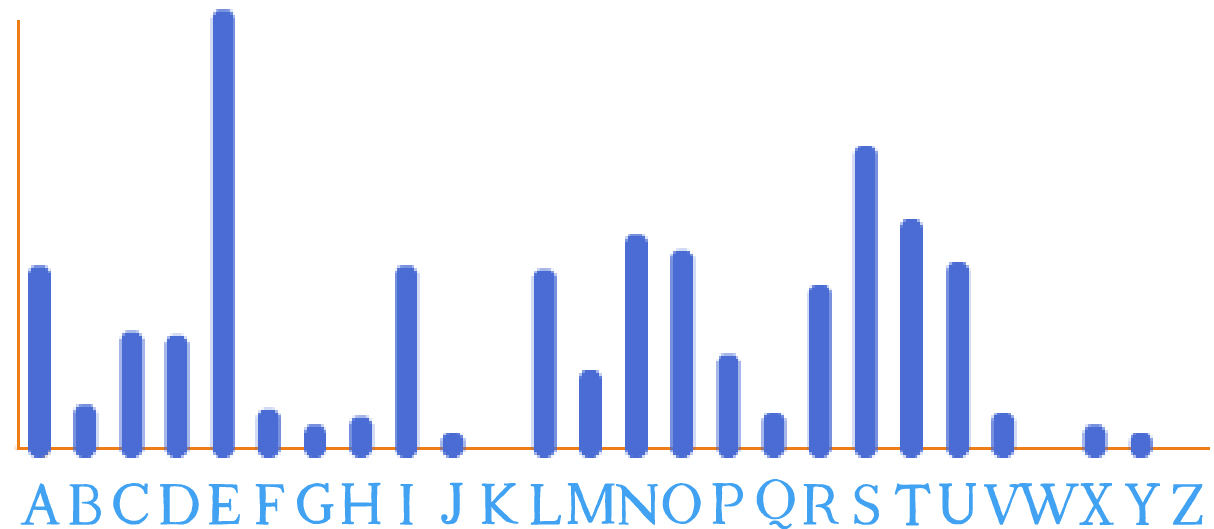
Note : ce graphique a été généré à l’aide du programme Scratch produit à la séquence 2.
Ici, l’axe n’est pas gradué car seule la forme générale de l’histogramme nous intéresse.
On remarque que, même pour ce texte relativement court, l’histogramme obtenu ressemble à celui du jeu de Scrabble© ou de l’histogramme de référence de la langue française. Il semble que, dès qu’un texte devient suffisamment long (de l’ordre de la centaine de lettres), on retrouve le schéma suivant :
- La lettre e est la plus fréquente. C’est la seule dont la fréquence dépasse 15%
- Elle est suivie des lettres a (9%), i (8%), s (8%), t (7%), n (7%) et r (6%)
- Seules huit lettres affichent une fréquence inférieure à 1% : f, h, j, k, w, x, y et z (onze lettres au total affichent une fréquence inférieure à 2 %)
Cryptanalyse pas à pas (par groupes ou collectivement)
Le professeur distribue aux élèves l’exercice 2 de la Fiche 6, qui propose d’effectuer la cryptanalyse d’un texte assez court (21 mots, 114 caractères, espaces et ponctuation non compris). La cryptanalyse est un exercice qui mêle mathématiques (analyse fréquentielle, basée sur la statistique) et linguistique (connaissance de la langue française, des lettres et des mots les plus fréquents, etc.).
ZRJ VDAARJ CLWJJRCK RK ERARMHRCK ZWIHRJ RK RULMP RC EHDWKJ. ZRJ EWJKWCBKWDCJ JDBWLZRJ CR FRMNRCK RKHR TDCERRJ GMR JMH Z'MKWZWKR BDAAMCR.
Notes scientifiques
- Contrairement à ce que l’on peut imaginer a priori, il est beaucoup plus facile de cryptanalyser un texte long qu’un texte court. Plus le texte est long, plus on se rapproche de l’histogramme de référence, et plus la statistique permet, seule ou quasiment, de cryptanalyser le texte.
- Avec un texte assez court, comme ici, il est nécessaire de faire de nombreux allers-retours entre la statistique et la linguistique pour parvenir à le cryptanalyser. Cependant, comme on le voit ci-dessous, on y arrive très bien !
Notes pédagogiques
- Réaliser, seul, un tel exercice pour la première fois est hors de portée d’élèves de collège. En revanche, réalisé collectivement (ou en petits groupes avec des temps de mise en commun), il permet d’acquérir la « gymnastique » permettant, ensuite, d’être plus autonome.
- En fonction de l’aisance des élèves, le professeur choisira de proposer cet exercice sous forme de défi (à réaliser en autonomie, par petits groupes). Dans tous les cas, il ne faudra pas hésiter à les guider s’ils sont bloqués. Pour cette raison, nous explicitons ci-dessous une méthode « pas à pas ».
Étape 1 : réaliser l’histogramme du texte
Cette étape, déjà réalisée à plusieurs reprises au cours de cette
séance, ne comporte plus aucune difficulté. Elle peut être réalisée
comme précédemment, chaque lettre étant comptée par un élève.
On obtient :
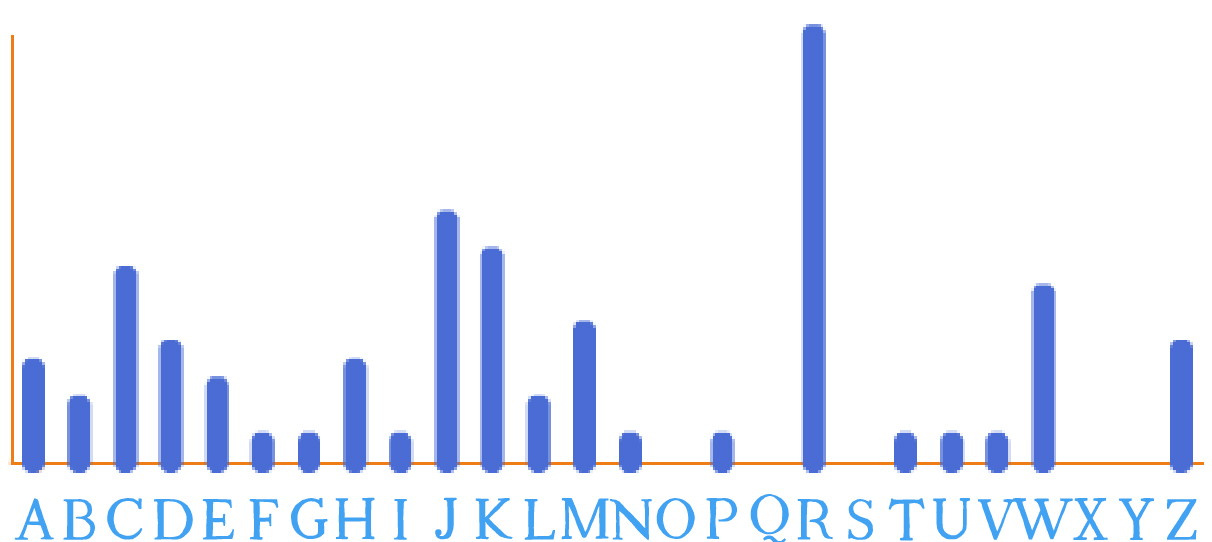
Étape 2 : chercher la lettre la plus fréquente
Une lettre se détache très nettement (le « R »), suivie par
4-5 lettres de fréquence élevée, tandis que 13 lettres ont une
fréquence très faible. Le schéma semble similaire à l’histogramme de
référence, on peut donc supposer que le texte clair est écrit en
français (ou en anglais, en allemand, en espagnol… qui ont des
histogrammes assez semblables, comme le montre la Fiche 7).
Dans ce cas, on peut faire l’hypothèse (raisonnable) que le « R » chiffre la lettre « e ».
Si l’on remplace les « R » par des « e », le message devient :
ZeJ VDAAeJ CLWJJeCK eK EeAeMHeCK ZWIHeJ eK eULMP eC EHDWKJ. ZeJ EWJKWCBKWDCJ JDBWLZeJ Ce FeMNeCK eKHe TDCEeeJ GMe JMH Z'MKWZWKe BDAAMCe.
Étape 3 : chercher les mots courts
Ici, pour rendre le travail plus facile, on a laissé les espaces et
la ponctuation… ce qui permet de rechercher les mots courts, peu
nombreux.
Il y a 2 mots de 2 lettres dans ce message : eK (répété 2 fois),
eC et Ce. En français, les mots de 2 lettres les plus fréquents
sont (dans l’ordre) : de, il, le, et, je, la, ne, un, en, ce,
se, sa, du. Etant donnée la position de la lettre « e » dans
les mots de 2 lettres présents ici, on peut faire l’hypothèse que :
- « eK » correspond à « et » (K→ t)
- « eC » pourrait correspondre à « en » (C →n). « Ce » correspond à « de » ou « le » ou « ne » (C → d ou C → l ou C →n). On peut donc faire l’hypothèse que C →n.
Selon cette hypothèse, le texte devient :
ZeJ VDAAeJ nLWJJent et EeAeMHent ZWIHeJ et eULMP en EHDWtJ. ZeJ EWJtWnBtWDnJ JDBWLZeJ ne FeMNent etHe TDnEeeJ GMe JMH Z'MtWZWte BDAAMne.
On commence à reconnaître des structures familières (les 3ème, 5ème
et 15ème mots finissent par « ent », comme un verbe à la 3ème
personne du pluriel), ce qui nous encourage à poursuivre : notre
hypothèse, jusque-là, semble correcte !
Note pédagogique
Obtenir la liste des mots de 2 ou 3 lettres en langue française est
aisé… car c’est un sujet qui intéresse les amateurs de Scrabble© !
Voir ici, par exemple : www.listesdemots.com
Dans le même esprit, on peut rechercher les mots de 3 lettres. Le
texte en compte 3 : ZeJ (répété 2 fois), GMe et JMH. En français,
les mots de 3 lettres les plus fréquents sont (dans l’ordre) : que,
les, son, mon, pas, lui, une, des, qui, est. Notre mot
« ZeJ » pourrait bien être « les » (plus probable,
car plus fréquent) ou « des ».
Si l’on fait l’hypothèse que ZeJ →les (Z → l et J → s), notre texte devient :
les VDAAes nLWssent et EeAeMHent lWIHes et eULMP en EHDWts. les EWstWnBtWDns sDBWLles ne FeMNent etHe TDnEees GMe sMH l'MtWlWte BDAAMne.
Et si GMe → que (mot de 3 lettres finissant par e le plus fréquent), alors le texte devient (avec G → q et M →u) :
les VDAAes nLWssent et EeAeuHent lWIHes et eULuP en EHDWts. les EWstWnBtWDns sDBWLles ne FeuNent etHe TDnEees que suH l'utWlWte BDAAune.
Étape 4 : chercher les doublets
Les paires de lettres répétées sont souvent très utiles pour
cryptanalyser un tel texte. Les doublets présents dans le texte
sont : AA (répété 2 fois) et ss (en clair, car on l’a déjà
déchiffré). En français, les doublets les plus fréquents sont : ss,
ll, mm, rr, tt, nn, pp, ee, cc et ff.
Puisque les lettres s et l sont déjà trouvées, on peut essayer de remplacer AA par mm. Donc, si A → m, le texte devient :
les VDmmes nLWssent et EemeuHent lWIHes et eULuP en EHDWts. les EWstWnBtWDns sDBWLles ne FeuNent etHe TDnEees que suH l'utWlWte BDmmune.
Étape 5 : revenir au tableau de fréquences
Les lettres que nous avons déjà trouvées sont :
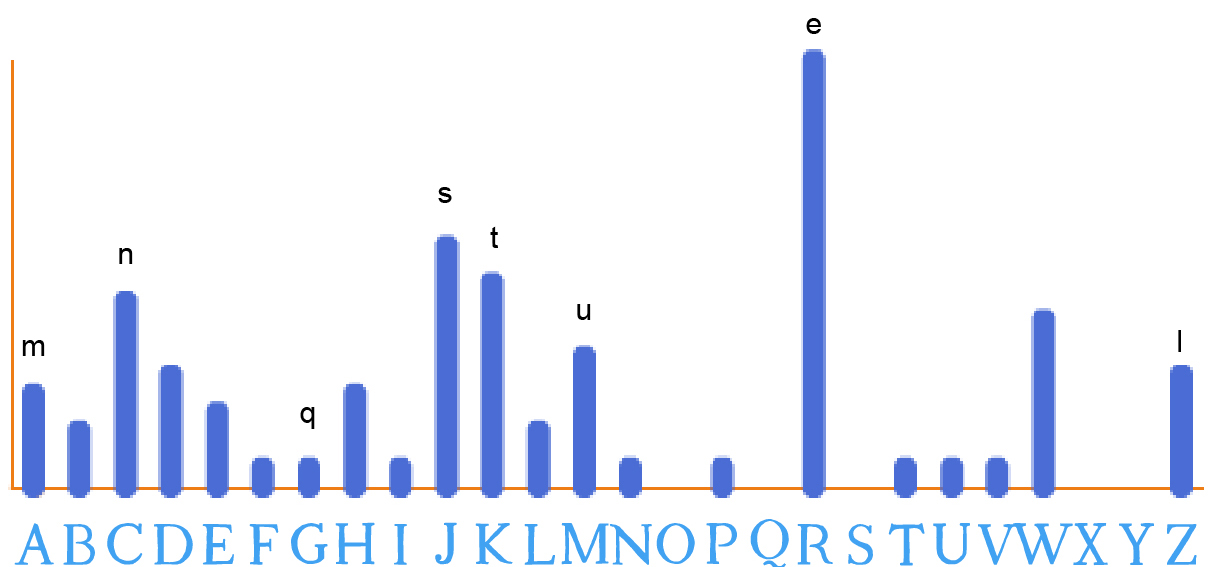
Or, on sait qu’en français, après la lettre e, les lettres les plus
fréquentes sont a, i, s, t. Puisque s et t ont été trouvées (et
correspondent bien à des pics), il est fort probable que a et i soient
cachées derrière la lettre la plus fréquente restante (W).
Si on fait l’hypothèse que W →a, alors le texte devient :
les VDmmes nLassent et EemeuHent laIHes et eULuP en EHDats. les EastanBtaDns sDBaLles ne FeuNent etHe TDnEees que suH l'utalate BDmmune.
Le 3ème mot ne semble pas exister en français, ni l’avant dernier. L’hypothèse ne semble pas justifiée. Essayons W → i. Le texte devient :
les VDmmes nLissent et EemeuHent liIHes et eULuP en EHDits. les EistinBtiDns sDBiLles ne FeuNent etHe TDnEees que suH l'utilite BDmmune.
Formidable ! On reconnaît le mot « utilité » à l’avant-dernière place en partant de la fin.
Le 3ème mot « nLissent » pourrait être « naissent ». Dans ce cas, L → a, ce qui donne :
les VDmmes naissent et EemeuHent liIHes et eUauP en EHDits. les EistinBtiDns sDBiales ne FeuNent etHe TDnEees que suH l'utilite BDmmune.
De retour à l’histogramme des fréquences, parmi les lettres les plus fréquentes (a, i, s, t, n et r), il ne nous reste plus que r à trouver. Le pic restant pourrait correspondre à H ou C. C a déjà été trouvé (il correspond à n). Reste H. Si H → r. Alors, le texte devient :
les VDmmes naissent et Eemeurent liIres et eUauP en ErDits. les EistinBtiDns sDBiales ne FeuNent etre TDnEees que sur l'utilite BDmmune.
On reconnait les mots « être » et « sur » dans la seconde phrase (remarque : on aurait pu trouver cela en regardant les mots de 3 lettres qui commencent par « su »… il y avait des chances pour que cela soit « sur » !). Le 6ème mot de la première phrase pourrait bien être « libre ». Dans ce cas (l → b), on aurait :
les VDmmes naissent et Eemeurent libres et eUauP en ErDits. les EistinBtiDns sDBiales ne FeuNent etre TDnEees que sur l'utilite BDmmune.
Dès lors, le déchiffrement devient très facile : le 5ème mot est « demeurent » (E → d).
les VDmmes naissent et demeurent libres et eUauP en drDits. les distinBtiDns sDBiales ne FeuNent etre TDndees que sur l'utilite BDmmune.
Le contexte nous aide : le second mot est probablement « homme », et le dernier mot de la première phrase « droit ». Dans ce cas (V → h, D → o), on a :
les hommes naissent et demeurent libres et eUauP en droits. les distinBtions soBiales ne FeuNent etre Tondees que sur l'utilite Bommune.
Le travail est quasi-achevé, il suffit de considérer que le 8ème mot est « égaux » (U → g et P → x). Plus loin, on devine « distinctions sociales » (B → c). La dernière étape est :
les hommes naissent et demeurent libres et egaux en droits. les distinctions sociales ne FeuNent etre Tondees que sur l'utilite commune.
Par élimination, on en déduit que « Feuvent » correspond à
« peuvent » et « Tondees » à « fondees ».
Nous avons donc réussi, sans connaître la clé, à cryptanalyser ce
texte, malgré les millions de milliards de milliards de clés
possibles !
Ce texte est bien sûr le premier article de la déclaration des droits de l’homme (sans les accents) : les
hommes naissent et demeurent libres et egaux en droits. Les
distinctions sociales ne peuvent etre fondees que sur l'utilite commune.
Quelle était la clé ?
Une fois la cryptanalyse terminée, il est très simple de trouver la clé. On connaît quasiment toutes les correspondances entre les 2 alphabets (clair et chiffré).
|
Alphabet clair |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
|
Alphabet chiffré |
L |
I |
B |
E |
R |
T |
U |
V |
W |
? |
? |
Z |
A |
C |
D |
F |
G |
H |
J |
K |
M |
N |
? |
P |
? |
? |
Les quelques cases restantes sont très faciles à remplir.
La clé est donc : LIBERT (le mot-clé était LIBERTE).
Note scientifique :
D’autres statistiques peuvent nous guider pour l’analyse fréquentielle. Par exemple :
- La fréquence des lettres en fonction de leur position dans les mots. En anglais, les mots commencent bien plus souvent par les lettres « t », « a » ou « s » que par « e », même si « e » est la lettre la plus courante.
- La fréquence des paires de lettres ou « bigrammes ». En français, les bigrammes les plus fréquents sont « es », « de », « le », « en » et « re ». La recherche des « bigrammes » et des « trigrammes » (les plus fréquents sont « ent » et « les ») s’impose dès lors que le texte ne contient plus d’espace ni de ponctuation pour séparer les mots (rappel : nous avons gardé, ici, les espaces et la ponctuation par souci de simplification). Attention cependant : certains bigrammes apparents n’existent pas car ils sont à cheval sur 2 mots !
Etude documentaire (individuellement)
Le professeur distribue la Fiche 8 à chaque élève. La fiche est lue individuellement, puis discutée en classe entière. Cette discussion permet notamment de faire ressortir :
- La faiblesse de certaines méthodes de chiffrement qui, bien que proposant un nombre de clés très important, peuvent être cassées avec un peu d’astuce…
- La course permanente entre les cryptographes et les cryptanalystes
- Les enjeux actuels de la cryptographie (enjeux qui seront débattus plus en détail à la fin du projet).
Conclusion
La classe élabore une conclusion collective qui peut être, par exemple :
- L’algorithme est le plus important. Mieux vaut un bon algorithme et une machine médiocre qu’un algorithme médiocre et une bonne machine !
- L’analyse fréquentielle nécessite de faire des allers-retours entre la statistique et la connaissance de la langue (linguistique)
Prolongements EPI
En français :
- Lire « les hommes dansants », une des 56 nouvelles d'Arthur Conan Doyle mettant en scène le détective Sherlock Holmes. La cryptanalyse est au cœur de cette nouvelle (cf. prolongement en mathématiques proposé ci-dessous).
- Étudier quelques textes et remarquer que l’histogramme des fréquences peut varier sensiblement selon le registre de langage (familier, soutenu, etc.). Remarquer aussi que, dans un texte aussi atypique que « La disparition » de G. Perec, l’histogramme des fréquences ressemble tout de même fortement à l’histogramme de référence pour la langue française, mis à part le « e » qui a disparu.
En langue vivante :
- Étudier quelques textes et remarquer que les fréquences des lettres sont différentes de celles de la langue française (cependant, la lettre « e » reste largement dominante dans toutes ces langues, comme on le voit sur la Fiche 7).
En histoire :
- Étudier les conditions qui ont permis l’essor des sciences arabes, au point de parler d’un « âge d’or » : stabilité politique, prospérité économique, tolérance religieuse…
En mathématiques :
- Pour comprendre que l’analyse de fréquence marche quels que
soient les symboles utilisés (pas seulement des lettres), faire la
cryptanalyse d’un « texte » composé d’une suite de dessins.
Par exemple, un des messages figurant dans la nouvelle « Les hommes
dansants » (cf. prolongement en français proposé ci-dessus) :
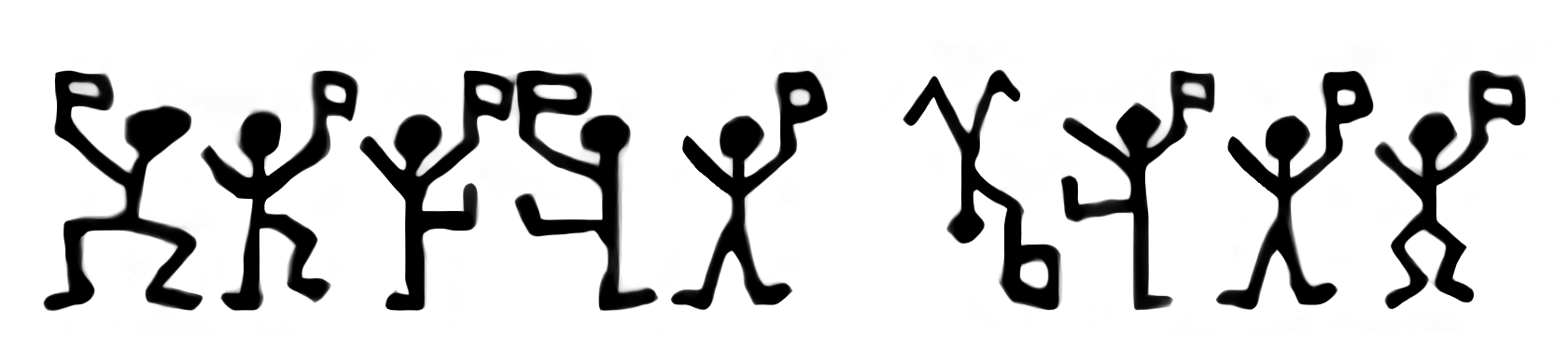
- Pour aller au-delà du chiffrement mono-alphabétique, on peut étudier :
Le chiffrement de Vigenère (le chiffrement utilise plusieurs alphabets différents)
Le chiffrement de Playfair (le chiffrement se fait par bigrammes, et non par lettres individuelles)
Extrait de "1, 2, 3... codez !", Editions Le Pommier, 2016-2017. Publié sous licence CC by-nc-nd 3.0.
