Nous savons aujourd’hui que les algorithmes peuvent tous s'écrire avec quelques instructions élémentaires qui sont assemblées à l'aide de structures de contrôle.
L'instruction élémentaire la plus courante est l'affectation d'une variable, par exemple a = 3 dont l'exécution consiste à affecter la variable a avec la valeur 3. Cette notion d'affectation d'une variable demande donc de comprendre le concept de variable : boîte qui contient une valeur que l'on peut utiliser et modifier au cours de l'exécution du programme.
Le nombre de fois où une vidéo a été visionnée sur une plateforme de streaming est un exemple de variable. À chaque fois que la vidéo est visionnée, la variable « nombre de vues » est modifiée (par exemple, l'instruction nombre de vues = nombre de vues + 1 permet d'affecter à la variable nombre de vues sa nouvelle valeur, soit un de plus).
D'autres instructions élémentaires sont l'affichage d'un message à l'écran, le déplacement d'un lutin, etc.

Ces instructions élémentaires sont ensuite assemblées avec des structures de contrôle, qui permettent de fabriquer des instructions complexes en assemblant des instructions plus simples. Les principales sont :

• la séquence : exécuter une instruction puis une autre ;
• le test qui permet d'effectuer une instruction ou une autre, en fonction d'une condition. Par exemple, dans un lave-linge, si le poids du linge est inférieur à 2 kg alors lancer le programme économique, sinon lancer le programme classique.
• la boucle, qui permet de répéter une instruction plusieurs fois.

Mais d'autres structures de contrôles existent, par exemple en programmation événementielle (en particulier dans Scratch), le déclenchement d'une instruction à la suite de la survenue d'un événement.

Les premiers ordinateurs sont capables d'exécuter des algorithmes composés de ces ingrédients… ce sont donc des machines capables d'exécuter tous les algorithmes du monde : des machines universelles. Gageons que pour les pionniers de l’informatique, voir s'incarner les algorithmes dans des machines universelles devait être exaltant.
Comme ces pionniers, l’apprenti programmeur découvre les capacités de son ordinateur de façon progressive. Il commence avec des algorithmes simples bien connus comme des opérations mathématiques (l'addition, la multiplication, etc.). Ensuite, les algorithmes se complexifient, reproduisant des suites mathématiques comme celle de Fibonacci ou de Bernoulli. Justement, c'est en écrivant un programme pour calculer la suite de Bernoulli sur la machine analytique de Babbage qu’Ada Lovelace est devenue la première personne au monde à écrire un programme informatique.

Il existe bien d’autres programmes encore. La machine universelle nous permet d’appliquer des algorithmes connus, mais également de rechercher des algorithmes pour résoudre des problèmes qu'on ne sait pas encore résoudre. Cependant, le fait que l’on trouve un algorithme signifie-t-il forcément que cet algorithme nous donnera toujours une solution ? Pour y voir plus clair, explorons ce que l’on appelle la « pensée informatique ».

La pensée informatique (voir à ce sujet l'article correspondant sur Interstices) est un ensemble de connaissances et d'attitudes mises en œuvre pour comprendre le monde qui nous entoure et nous aider à diriger nos actions. Elle couvre une vaste étendue de concepts, et nous allons tenter d'en éclairer ici quelques-uns.

Tout un chacun applique, tous les jours, des algorithmes … parfois sans le réaliser vraiment. Nous avons établi des stratégies, des habitudes, des raisonnements que nous appliquons à nos activités du quotidien. Dans un magasin, un samedi de courses, on peut choisir de parcourir les allées du début à la fin du magasin en vérifiant, pour chaque allée, si elle contient un produit qui est sur sa liste de courses. Mais pourquoi ne pas se faciliter la vie en rédigeant cette liste au préalable, en fonction de sa connaissance du magasin, pour que la liste présente les produits dans le bon ordre?  Pour aller travailler, on peut prévoir son trajet en fonction du jour de la semaine parce qu’il est connu que le mardi et le jeudi il faut absolument éviter la rue Kolmogorov qui est saturée. Enfin, quand on cherche un mot dans un dictionnaire, on l’ouvre à l'endroit le plus probable en fonction de la position de la première lettre de ce mot dans l'alphabet (vers le début pour la lettre 'c' ou vers le milieu pour la lettre 'p', etc.)… puis, par tâtonnements, on recule ou avance de quelques pages, en fonction de la lettre qui débute les mots de la page courante. Et lorsque la première lettre du mot est trouvée, on recommence avec la seconde lettre,  et ainsi de suite.

Les ordinateurs peuvent nous aider à traiter ces tâches quotidiennes ! Il s'agit alors de poser le problème de manière formelle, puis d'écrire un algorithme basé sur les quatre ingrédients vus plus haut (instructions, boucles, tests et variables) et permettant de le résoudre. Pour automatiser l’exécution de ces algorithmes, il faut les traduire en programmes et laisser une machine dérouler leurs instructions. Une partie de la pensée informatique consiste à rationaliser de tels procédés pour qu'une machine soit capable de le mettre en œuvre. Voyons maintenant quelles sortes de défis nous pouvons résoudre grâce à la pensée informatique et aux algorithmes. Il y a les défis que l'on peut résoudre avec des algorithmes qui s'inspirent du raisonnement humain. Ce sont des algorithmes comme, par exemple, celui qui établit la liste des courses dans l'ordre des allées du magasin. Beaucoup d'algorithmes sont conçus de cette manière. La personne qui met au point l'algorithme essaye de formaliser son propre raisonnement. C'est un peu comme expliquer la méthode à quelqu'un d'autre, mais en voulant s'assurer qu'il n'y aura aucune erreur d’interprétation. Ensuite, il y a les défis que l'on va résoudre avec un algorithme inspiré du raisonnement ou des pratiques humaines, mais en y ajoutant une étude qui permet de rendre l'approche plus rigoureuse et plus générale. Reprenons l'exemple de la recherche d’un mot dans le dictionnaire. Il existe un exercice très similaire qui consiste à chercher son nom, ou son prénom, dans une liste (par exemple, pour savoir si on est reçu à un concours). Essayons de formaliser la manière dont on réalise cette tâche.

Imaginons une liste,  non triée, de quelques dizaines de prénoms. Il faudra à tout un chacun une poignée de secondes pour y retrouver son nom (ou être sûr qu’il n’y est pas). Dans un second temps, si l’on fournit la même triée par ordre alphabétique, l’exercice est beaucoup plus rapide !
Cette différence d'efficacité vient du fait que, quand la liste est triée, il existe une méthode qui est bien plus efficace que si la liste n'est pas triée. Quand elle n'est pas triée, on peut chercher  un peu partout au hasard, ou bien on parcourt systématiquement la liste du début à la fin en vérifiant les prénoms un par un. En revanche, quand la liste est triée, on repère l’endroit où se trouvent les prénoms qui commencent par la première lettre de son prénom. Ensuite la deuxième lettre, etc.

Cette approche fonctionne, mais peut encore être perfectionnée. Car si le nombre d'objets est très grand (comme dans un dictionnaire, voire un répertoire téléphonique national avec des millions d’entrées) alors on peut faire de grands bonds en avant ou en arrière pour gagner du temps. Il existe un algorithme de recherche dans une liste triée très efficace (le plus efficace connu pour répondre à ce défi) : la « dichotomie », qui tire son nom du Grec pour l'expression « couper en deux ». Pour trouver un item dans une liste triée, on coupe la liste en son milieu ; si l’item était au milieu, on l’a trouvé, sinon on sait dans quelle moitié de la liste triée il se trouve ; on recommence donc la dichotomie sur la demie liste restante. Et ainsi de suite. À chaque étape, la liste dans laquelle on cherche l'information est deux fois plus petite.

Une liste de 20 prénoms est fouillée en 4 coups dans le pire des cas : le nombre d'opérations dans le pire des cas est donné par le nombre de fois qu'on peut diviser 20 par 2 avant d'arriver à 1 (on arrondit la première division si le nombre de cases est impair). Sans dichotomie, il aurait fallu (dans le pire des cas) 20 itérations pour lire successivement chaque prénom, du premier au dernier, pour se rendre compte que le sien n’y était pas. La puissance de la dichotomie se voit vite dans le cas de listes bien plus longues : une liste de 300 000 items est fouillée par dichotomie en 19 opérations seulement. Imaginons maintenant que chaque opération de lecture dans le tableau demande une milliseconde à l’ordinateur. Le tableau suivant estime le temps d’application des deux algorithmes dans le pire des cas :

Comparaison du temps mis, dans le pire des cas, pour rechercher un prénom dans une liste triée, à l’aide de 2 algorithmes différents. L’algorithme le plus simple (on parcourt la liste du début à la fin) met 10 000 fois plus de temps pour s’exécuter si la taille de la liste est multipliée par 10 000 (on passe de 3 dixièmes de seconde à 1 heure) ; tandis que la recherche dichotomique n’est rallongée que d’un centième de seconde.

Les approches pour mettre au point des algorithmes sont nombreuses. Nous ne pouvons pas les passer toutes en revue ici. En revanche, il est important de se pencher sur un type de défis en particulier, pour lesquels on sait écrire un algorithme correct, mais qui ne connaîtront pourtant jamais de solution. Ou plutôt devrions-nous dire qu'on n'obtiendra pas la solution en un temps raisonnable. Il s'agit là d'un aspect fondamental de l'algorithmique. Considérons par exemple le « problème du voyageur de commerce » que nous décrivons lors d’une séance débranchée pour le cycle 3 (séance III-2.5). Il s'agit de trouver, pour un ensemble de villes dans lesquelles doit se rendre un voyageur de commerce, l'ordre dans lequel visiter ces villes de façon à passer le moins de temps possible sur la route. S’il n’y a que 2 villes à visiter, la réponse est simple, avec un seul trajet possible pour les relier. Avec 3 villes, il y a 6 trajets possibles à comparer (dans ce décompte, on distingue des trajets « identiques » mais parcourus dans 2 sens différents, par exemple Lyon-Bordeaux-Marseille et Marseille-Bordeaux-Lyon). Avec 4 villes, il y a 24 trajets possibles. Avec 20 villes, il y a déjà plus de deux milliards de milliards de possibilités. Un ordinateur mettrait plusieurs milliards d’années à tester toutes les possibilités pour y trouver à coup sûr la meilleure ! Ce problème se retrouve dans de nombreuses applications comme la tournée du facteur (ou des éboueurs, des déneigeuses…) : dans quel ordre parcourir les rues dans lesquelles il faut passer ? Il s'agit du même problème que celui dans les usines où des bras articulés (des robots) doivent visser des boulons sur une plaque à différents endroits : dans quel ordre visser les boulons pour minimiser les déplacements et donc économiser de l'énergie et la durée de vie du robot ? Quand le nombre « d'objets » augmente alors le nombre de possibilité explose. On parle d'explosion combinatoire ou de croissance exponentielle. Au-delà d'un nombre d'objets (rues, classes, boulons à fixer) relativement petit, la solution à tous ces problèmes est… tout simplement inconnue !

Bien entendu, pour réduire le temps de calcul, on peut envisager de prendre un ordinateur plus performant ou un autre langage plus efficace. Le nouveau programme, écrit par un programmeur expérimenté dans un langage plus performant, sera peut-être dix fois ou même cent fois plus rapide. Mais, quand le temps de calcul est estimé à 10 milliards d'années, on passera peut-être à « seulement » cent millions d'années. Imaginons même, pour la beauté du raisonnement, qu’on trouve une architecture informatique, un langage de programmation, un système qui permette de calculer la solution exacte au trajet entre 20 villes en une minute. Que se passera-t-il si le problème initial changeait un peu ? Ajoutons une ville : il mettra une minute pour chacune des 21 villes, donc 21 minutes pour trouver la solution. Ajoutons une seconde ville : le super-ordinateur tourne pendant 7 heures. Une troisième ville ? Le calcul dépasse 7 jours. Cette machine imaginaire, et déjà totalement hors de portée, se trouve ainsi mise à mal avec seulement quelques items supplémentaires.

Toutefois, la situation n'est pas désespérée car il existe plusieurs méthodes pour répondre à ces défis, mais elles ne calculent pas la solution exacte. On propose une solution qui paraît convenable, on l'améliore plusieurs fois, et quand on pense que c'est trop difficile de faire mieux alors on en reste là en estimant que ce n'est déjà pas si mal. En informatique une telle approche, donnant un résultat satisfaisant mais non optimal, est appelée une heuristique. Cela revient un peu à appliquer l'adage qui veut que « le mieux est l'ennemi du bien ». Savoir reconnaître ces problèmes pour lesquels on ne peut pas calculer de solution en un temps raisonnable est un aspect majeur de l'algorithmique. Si un programme est très long à s'exécuter ce n'est peut-être pas à cause d'un bug ou d'une mauvaise connaissance du langage. C'est peut-être simplement parce que l'algorithme est correct, tout comme le programme, mais… qu’il peut met beaucoup de temps à s’exécuter.

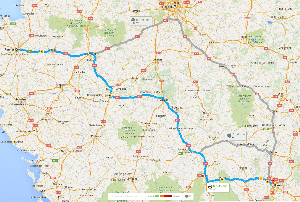
Ce chemin proposé pour relier Nantes et Lyon n’est pas le meilleur chemin possible : le trouver nécessiterait des milliards d’années de calcul. C’est une heuristique, un compromis entre la qualité du chemin et le temps de calcul alloué à sa recherche. Le meilleur chemin n’est probablement pas beaucoup plus court que celui-ci. © GoogleMaps

Bien entendu, cela ne signifie pas que l'on peut se passer de programmeurs expérimentés qui connaissent bien le fonctionnement de leurs langages préférés, ni que les progrès technologiques sont sans importance. Beaucoup seront satisfaits de voir les performances de leur logiciel préféré améliorées par une programmation judicieuse ou un processeur plus rapide. Mais les progrès de l'algorithmique sont indispensables à une meilleure connaissance de la nature des problèmes que l'on aborde et de la manière dont on peut les résoudre… ou pas !