Comment représenter un nombre ?

Une branche entière de l'informatique s'intéresse à la représentation des données sous la forme d'une suite de symboles pris dans un alphabet fini, souvent dans un alphabet qui ne contient que deux caractères : 0 et 1.  Ainsi, pour représenter les nombres entiers dans un alphabet qui ne contient que ces deux caractères, on peut associer une suite de quatre caractères « 0 ou 1 » à chaque chiffre, par exemple :

• 0 : 0000
• 1 : 0001
• 2 : 0010
• 3 : 0011
• 4 : 0100
• 5 : 0101
• 6 : 0110
• 7 : 0111
• 8 : 1000
• 9 : 1001

Puis, pour représenter un nombre, la première idée, intuitive, qu’on peut avoir consiste à juxtaposer la représentation de chacun de ses chiffres. Le nombre 13 par exemple se représente alors en juxtaposant la représentation 0001 du chiffre 1 avec la représentation 0011 du chiffre 3 : 00010011. Cette notation, peu compacte, n’est pas utilisée en pratique pour les nombres.

Une autre représentation plus concise consiste à représenter le nombre en base deux. Le nombre 13 par exemple, qui se décompose en une unité, zéro paquet de deux unités, un paquet de deux paquets de deux unités et un paquet de deux paquets de deux paquets de deux unités (1 + 4 + 8) s'écrit de droite à gauche : 1-0-1-1, soit 1101 de gauche à droite.

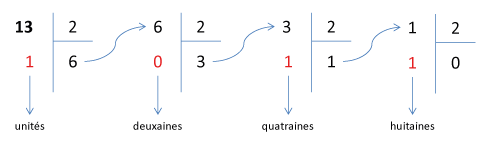
Pour écrire le nombre 13 en base 2, on  doit le décomposer comme une somme de puissances de 2.
Pour cela, il faut effectuer une série de divisions par 2, jusqu’à obtenir un quotient égal à 0.
Les chiffres (qui sont les restes des divisions) doivent alors être remis dans l’ordre (unités à gauche).

Une succession de 64 caractères « 0 ou 1 » permet alors de représenter les nombres de 0 à 2⁶⁴ - 1 = 18 446 744 073 709 551 615. La question de la représentation des nombres ne s'arrête cependant pas là, car les nombres négatifs et les nombres décimaux ont leur propre mode de représentation.

Comment représenter un texte ?

La représentation des caractères textuels – et des textes qui sont des successions de caractères textuels – est aussi une question très riche. Une première idée pour représenter les caractères textuels était d'associer un groupe de 7 caractères « 0 ou 1 » à chaque caractère d'un alphabet qui en contenait 95 (26 minuscules, 26 majuscules, 10 chiffres et 33 autres symboles, incluant les signes de ponctuation). Le caractère textuel « a » était représenté par 1100001, « b » par le 1100010, etc. Et un mot était simplement représenté par la juxtaposition de la représentation de ses caractères – ses lettres. Le mot « Le » par exemple était représenté par la juxtaposition de la représentation 1001100 du caractère « L » et la représentation 1100101 du caractère « e » : 10011001100101.

Mais cette représentation, appelée American Standard Code for Information Interchange (ASCII), était adaptée à l'anglais et non aux langues qui, comme le français, utilisent des signes diacritiques : accents, cédilles, ...  La représentation ASCII a donc été étendue plusieurs fois pour arriver à la représentation Unicode, qui permet de représenter les quelques 110 000 caractères utilisés par les différentes écritures du monde, y compris les écritures non alphabétiques, comme le chinois.

Comment représenter une image ?

La représentation des images est plus difficile et elle repose sur un découpage de l'image en pixels, puis par un codage de la teinte de chaque pixel. Dans une image en noir en blanc, chaque pixel est représenté par un seul « 0 ou 1 » : 1 s'il est noir, 0 s'il est blanc.

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 1 1 1 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

A gauche, une image noir et blanc de 16x16 pixels. À droite, le codage binaire de cette image.
Pour faciliter la lecture, on a disposé les bits sur une grille 16x16.

Dans une image en niveaux de gris chaque pixel est classiquement représenté par un nombre compris entre 0 et 255, lui-même représenté en base deux par un groupe de huit « 0 ou 1 », 0 = 00000000 s'il est noir, 1 = 00000001 s'il est gris foncé, ... 254 = 11111110 s'il est gris clair, 255 = 11111111 s'il est blanc. Bien entendu, le choix d'utiliser 255 niveaux de gris est arbitraire et d'autres formats existent.

Dans une image en couleur, chaque pixel est classiquement représenté par trois nombres, chacun compris entre 0 et 255 qui indiquent la quantité de rouge, de vert et de bleu dans ce pixel. Par exemple un pixel rose bonbon est obtenu en mélangeant 249 unités de rouge, 66 unités de vert et 158 unités de bleu, le nombre 249 se représente en base deux par 11111001, le nombre 66 par 1000010 et le nombre 158 par 10011110, si bien qu'un pixel rose bonbon se représente par la succession de 18 « 0 ou 1 » : 11111001100001010011110.

Une image se représente naturellement en juxtaposant les représentations de chacun de ses pixels.  Si bien qu'une image formée de deux pixels rose bonbon se représente par : 1111100110000101001111011111001100001010011110.