L'histoire de l'informatique est celle d'une confluence. Deux courants de pensée, centrés l'un autour de la notion d'algorithme et l'autre autour de celle de machine, ont conflué dans les années 1940, pour aboutir à la conception des premiers ordinateurs, machines à exécuter des algorithmes. Deux autres courants de pensée, centrés autour des notions de langage et d'information, ont, par la suite, rejoint cette confluence.

L'histoire de la notion d'algorithme remonte aux débuts de l'écriture, puisque les premières traces écrites que nous avons retrouvées sont des calculs comptables : les scribes de Mésopotamie connaissaient donc des algorithmes pour effectuer des additions et des multiplications, mais aussi des opérations plus complexes comme des calculs d'intérêts composés, d'héritages… Il est même possible de faire remonter l'histoire de la notion d'algorithme plus tôt, en étendant la notion d'algorithme à des méthodes systématiques qui opèrent sur d'autres objets que de l'information, ce qui permet de concevoir les méthodes de fabrication du bronze ou de la céramique, les recettes de cuisine ou encore les procédés de tissage des étoffes comme des algorithmes. L'histoire de la notion de machine est ancienne, elle aussi, même si on la limite aux machines opérant sur de l'information, puisque les machines d'Héron d'Alexandrie, les carillons des cathédrales, les machines à calculer de Schickard, Pascal, Leibniz, le métier à tisser de Jacquard… contiennent déjà des ébauches de traitement de l'information.

L'histoire de l'informatique est foisonnante et s’étale sur de nombreuses années ou siècles. Voici une sélection de personnages qui sont associés à cette histoire en marquant des jalons importants. Cette sélection permet d'expliquer des concepts de l'informatique en profitant de l'aspect attractif de l'approche historique pour véhiculer des concepts. Elle doit cependant être accompagnée d'une modération : il est délicat d'attribuer clairement telle ou telle contribution à une personne en particulier. Les découvertes se font en effet de manière incrémentale, chaque « inventeur » ayant construit sa propre contribution grâce à celles de ses prédécesseurs et, souvent, de ses contemporains. Cette modération permet surtout de dire que ces personnes, aussi géniales ont-elles pu être, ne sont pas l'unique vecteur de ces contributions, mais qu'on peut tout à fait reconnaître l'importance majeure de leur travail comme une pierre angulaire.

Muhammad ibn Mûsâ Al Khwarizmi Johannes Gutenberg Joseph Marie Jacquard Charles Babbage Ada Lovelace Alan Turing Grace Hopper Une brève histoire du réseau Internet

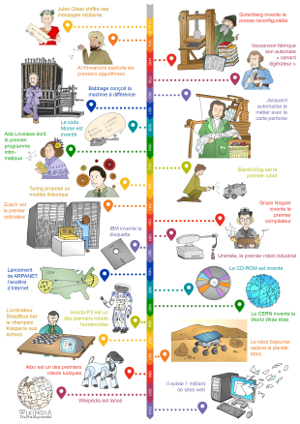La séance « Bilan : qu’est-ce que l’informatique ? » propose aux élèves de reconstituer une frise chronologique similaire à partir d’études documentaires portant sur l’histoire de l’informatique.

Muhammad ibn Mûsâ Al Khwarizmi

Al Khwarizmi est un savant Perse, vraisemblablement né dans les années 780. Il évolue dans un empire qui, sous le règne du calife Al-Mamum, encourage les sciences et les arts. Avec d'autres penseurs de son époque il travaille dans “la maison de la sagesse”, une école fondée par le calife à Bagdad pour étudier la géométrie, l'algèbre et l'astronomie. Ainsi, son travail consiste d'abord à traduire des manuscrits scientifiques ou philosophiques grecs et indiens. Avec ces travaux il transmet à ses contemporains les connaissances de ces civilisations, comme le système décimal de numération. Puis, Al Khwarizmi écrit ses propres textes scientifiques et en particulier l'ouvrage “Kitâb al-jabr wa al-muqâbala” dans lequel on peut entendre le son “al-jabr” qui est à l'origine du mot “algèbre”. Il cherche à  fournir des outils permettant de régler des problèmes de la vie quotidienne. Le mieux est encore de laisser Muhammad Al Khwarizmi expliquer lui-même que ses travaux sont destinés à faciliter les calculs « dont ont besoin les gens dans leurs héritages, dans leurs donations, dans leurs partages, dans leurs jugements, dans leurs commerces et dans toutes les transactions qu'il y a entre eux à propos de l'arpentage des terres, du creusement des canaux, de la géométrie et d'autres choses relatives à ses aspects et à ses arts (…) ».

 La marque d'Al Khwarizmi dans l'histoire est fortement liée à celle des mathématiques avec ses travaux sur l'algèbre et la géométrie. Mais son nom est également indissociable de l'informatique car chaque procédure qu'il décrit pour résoudre un calcul est un enchaînement d'instructions qui sont des manipulations sur des nombres. D'ailleurs, le nom d'Al Khwarizmi, a été traduit par “Algorismi” en Latin, et donnera plus tard le mot “Algorithme”.
 

Johannes Gutenberg

Johannes Gutenberg nait vers l'an 1400 à Mayence, en Allemagne. Il apprend l'orfèvrerie puis met son expérience dans le travail des métaux au service de son invention : l'imprimerie. L'histoire de l'imprimerie précède toutefois largement celle de Gutenberg. Cette histoire, qui reflète l'importance pour l'humanité de rendre ses œuvres durables et d'en assurer la diffusion, remonte au VIIe siècle. Des gravures sur planches de bois sont alors utilisées pour reproduire des textes et des images sur des pages de papier ou de tissus. Les procédés permettant de reproduire une page à l'identique évitent de faire ce travail manuellement et connaissent beaucoup de progrès. Le plus significatif de ces progrès est probablement l'invention par Bi Sheng du caractère mobile d'imprimerie, dont on retrouve les premières traces en Chine, vers 1040. Ces caractères sont alors en terre cuite puis ils évoluent vers le métal. En Europe, Gutenberg applique un principe habituel dans l'histoire des inventions : il perfectionne des techniques existantes et les combine. Ainsi, il crée un alliage métallique qui s'avère très adapté pour l'imprimerie : le « plomb typographique ». Il propose également la « presse à imprimer », plus efficace que les techniques existantes pour appliquer la page sur la planche. Enfin, il met au point une encre plus épaisse et adaptée pour l'imprimerie. Son invention connaît un succès grandissant et se propage rapidement en Europe.

L’imprimerie, sans avoir directement influencé l'informatique, entretient avec elle des liens intéressants. Tout d'abord, parmi les innovations de l’imprimerie, penchons-nous sur le caractère mobile d'imprimerie. Il permet de remplir une page avec les caractères de son choix et de façon réversible, alors qu'avant, il fallait graver la page toute entière de manière irréversible. La planche devient donc reconfigurable. On peut de surcroît fournir une planche à une autre presse qui pourra à son tour (re)produire la même page. D'une certaine manière, le simple fait de rendre une machine configurable peut être vu comme un ancêtre lointain de la notion de programmation qu'on trouvera bien plus tard dans le métier à tisser de Jacquard, dans les machines de Babbage, et finalement dans les ordinateurs. Un autre lien important avec l'informatique se retrouve dans la révolution culturelle apportée par l'imprimerie. On estime qu'au XVIIIème siècle, le nombre total de livres imprimés était d'environ un milliard, ce qui a totalement changé l'accès au savoir et donc l'équilibre social.
 

Joseph Marie Jacquard

Joseph Marie Jacquard est un inventeur et mécanicien français né en 1752 à Lyon. Pour avoir été tisseur dans l’atelier de son père, il connaît bien le métier à tisser, qui permet de fabriquer des étoffes. Cet outil est alors très répandu, source d'emplois, mais sa manipulation est complexe. Elle mobilise plusieurs personnes pour faire passer les navettes (qui déroulent les fils) au bon moment dans la machine. Jacquard veut mécaniser le métier à tisser pour le rendre plus facile d'emploi et plus performant. Il reprend alors le système de ruban perforé que Basile Bouchon a ajouté au métier à tisser et la mécanisation proposée par Jacques Vaucanson. En améliorant et en combinant ces deux technologies, il contribue à l’expansion du métier à tisser. Le système de cartes perforées permet de définir sur un support solide les instructions de passage des navettes. Les cartes perforées sont ensuite placées dans le métier à tisser, qui les fait défiler à chaque étape de la confection du tissu. Quand une carte perforée passe dans le métier, l'emplacement des trous dans la carte fait changer la position des fils et guide le passage des navettes. Chaque façon de trouer la carte correspond à un passage différent, et donc à un motif précis sur le tissu. En multipliant les cartes perforées, il devient alors possible d'écrire les instructions pour obtenir le motif complet à l’échelle du lé entier.  Comme pour l'imprimerie de Gutenberg, le métier à tisser devient configurable. Un ensemble de cartes peut être copié à l'identique et utilisé sur un autre métier et cela donne exactement le même tissu avec les mêmes motifs. Le même métier avec un jeu de cartes perforées différent donne un autre tissu avec d'autres motifs.

L'invention de Jacquard permet de produire plus de tissus, plus rapidement : elle connaît un grand succès avec plus de 20 000 métiers construits. Parce qu'elle utilise des cartes perforées pour donner des instructions à une machine configurable, cette invention est considérée comme un des ancêtres de l'ordinateur. Le travail de Jacquard illustre bien le schéma habituel des innovations. Jacquard cherche son inspiration dans les technologies les plus avancées de son époque, comme par exemple le ruban perforé de Basile Bouchon. Il adapte et améliore plusieurs inventions pour les combiner en un seul mécanisme plus facile à installer et à utiliser. L'avancée majeure obtenue par Jacquard sur le métier à tisser permet sa manipulation par un seul ouvrier, au lieu de six précédemment. Ces ouvriers, appelés « Canuts » se sont révoltés par la suite en raison du manque de travail, souvent attribué à cette invention.

Mécanisme Jacquard (extrait d’un métier à tisser) exposé au musée des arts et métiers de Paris

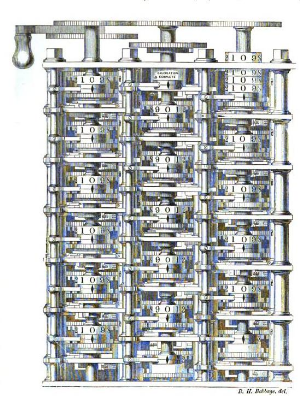
Charles Babbage

Charles Babbage, né en 1791, est un mathématicien et inventeur Britannique. À cette époque, bien avant l'invention du GPS, la navigation en mer se fait par l'observation de la position des étoiles dans le ciel, et par comparaison avec leur position attendue à cette date. Cette méthode permet de connaître la position du bateau  sur le globe terrestre.  Cela suppose de calculer, à l'avance, la carte du ciel jour après jour pour les semaines à venir. Malheureusement, les calculs sont longs et difficiles et les mathématiciens qui les réalisent risquent de se tromper, ce qui peut provoquer des accidents en mer. En 1821, Charles Babbage présente un projet de machine à la Société Royale d'Astronomie de Londres, pour accélérer ces calculs et les rendre plus fiables : la « machine à différences ». L'objectif de cette machine est de résoudre automatiquement, par un processus mécanique, ces calculs complexes permettant de prévoir la position des étoiles.

Ada Lovelace

Augusta Ada King (Ada Lovelace), est une mathématicienne Britannique née le 10 décembre 1815 à Londres. Elle est la fille de lord Byron, poète britannique, qu'elle n'a pas connu. Sa mère, qui tient à ce qu’Ada reçoive une éducation scientifique soutenue, lui fait particulièrement étudier les mathématiques. Cette éducation est assez atypique pour une jeune fille de cette époque. À 17 ans, Ada rencontre Charles Babbage et se passionne pour son travail sur la machine à différences, puis sur la machine analytique. Ada Lovelace et Charles Babbage forment un véritable duo scientifique. Ada écrit la plus complète des documentations sur la machine de Babbage et le soutient dans ses difficultés financières. Lui aide Ada à approfondir ses connaissances des mathématiques en lui recommandant d'étudier avec les plus célèbres mathématiciens du royaume.

Alors que Babbage prévoit l’utilisation de sa machine  pour des calculs numériques, Ada parle déjà d'une utilisation plus universelle. À l’époque, le calcul numérique est déjà traité de manière automatique par des machines comme la Pascaline : il s'agit d'un ensemble de rouages permettant de faire uniquement des additions et des soustractions. Pour Babbage, sa machine était une sorte de « calculatrice programmable » : on pouvait d'abord lui expliquer le calcul qu'elle devait faire (avec des instructions, le « programme ») puis lui donner les valeurs sur lesquelles appliquer ces instructions.
Visionnaire, Ada a su comprendre le potentiel de cette machine peut-être encore plus que Babbage lui-même. Elle décrit dans ses manuscrits la possibilité pour cette machine de manipuler des nombres, mais aussi des lettres ou n'importe quel type de symbole. Elle explique comment cette machine pourrait être programmée pour des tâches bien différentes du calcul numérique, comme la composition de morceaux de musique. Dans ses notes, Ada décrit l'ensemble des instructions qu'il faut donner à la machine de Babbage pour qu'elle réalise un calcul particulier : celui des termes successifs de la suite de Bernoulli. En réalisant cela, elle devient la première personne au monde à écrire un programme informatique. Autrement dit, le premier programmeur... est une programmeuse !
 

Alan Turing

Alan Turing est un mathématicien et informaticien britannique, né en 1912. Il est souvent présenté comme le père fondateur de l'informatique - bien qu'il soit sans doute vain de chercher un tel père fondateur à ce qui est une création collective. Ses contributions à l'informatique naissante sont multiples. Dans les années trente il donne l'une des premières définitions précises de la notion d'algorithme. Son objectif est alors d'étudier ce qui est « calculable ». Une multiplication, par exemple, est calculable car on peut la réaliser avec un certain nombre d'étapes. Mais quels sont les problèmes calculables ? C'est une question difficile, particulièrement étudiée dans les années 1930, sur laquelle Turing se penche. En étudiant cette question, il propose une machine abstraite, c'est-à-dire une machine qui n'est pas destinée à être fabriquée concrètement, mais qui va lui servir à structurer son raisonnement. Imaginer son fonctionnement lui permet de mieux étudier ce qui est calculable ou pas. Cette machine se décrit très simplement. Elle utilise un ruban qui contient une suite de cases dans lesquelles sont inscrites des données (des 0 et des 1). La machine est capable de lire ce qu'il y a dans les cases, de se déplacer sur le ruban d'une case à gauche ou à droite, et d'écrire dans une case. Avec cette machine, Turing montre qu'il est possible de remplacer n'importe quelle autre machine, en écrivant sur le ruban le « programme » de la machine remplacée (par exemple la multiplication) et ensuite les « données » sur lesquelles appliquer ce programme. Cette façon de mettre ensemble le programme et les données dans une machine est fondamentale et se trouve aujourd'hui dans tous les ordinateurs.

Durant la seconde guerre mondiale, Turing joue un rôle majeur dans la construction de machines électromécaniques permettant de déchiffrer les messages secrets utilisés par l'armée allemande, sans en connaître la clé. Après la guerre, il travaille à la conception des premiers ordinateurs britanniques au National Physical Laboratory, puis à l'Université de Manchester.

Machine de Turing réalisée en Légo® (projet Rubens, ENS Lyon) : vue globale (en haut) et détail de la tête de lecture -  écriture (en bas).

Il est aussi à l'origine de nombreuses autres idées sur le caractère phénoménologique de l'intelligence, sur la genèse des formes en biologie, sur la résolution approchée d'équations différentielles avec un ordinateur, ou sur les preuves de programmes. Dans ce dernier cas, la problématique est la suivante : on peut faire des tests sur un programme pour vérifier sa stabilité et son exactitude. Si on trouve une erreur, on cherche alors à réparer le programme ; mais si on ne trouve pas d’erreur par cette méthode, cela veut-il dire qu’il n’y a pas d’erreur, ou qu’on n’a pas su la trouver ? Existe-t-il une preuve mathématique que le programme est réellement sans erreur ?

Condamné à la castration chimique en raison de son homosexualité, considérée comme un crime dans l’Angleterre de cette époque, Alan Turing s'est suicidé à 41 ans.
 

Grace Hopper

Grace Hopper est une mathématicienne Américaine, née en 1906. Elle grandit en montrant une véritable curiosité pour les sciences et la technologie (par exemple, en démontant les réveils de sa maison les uns après les autres, jusqu'à arriver à en remonter un entièrement... à l’âge de 7 ans). Ses parents encouragent son goût pour les sciences tout en veillant à valoriser ses choix plutôt que suivre la tradition en matière d'éducation des jeunes filles Américaines. Ainsi, Grace sera une des rares femmes de son époque à étudier à l'université de Yale et à obtenir un doctorat de mathématiques. Pendant la deuxième guerre mondiale, elle entre dans la marine, où elle est nommée lieutenant, et rejoint l'équipe qui travaille sur le Mark 1, le premier ordinateur des États-Unis. Grace Hopper fait alors partie du premier groupe capable de programmer cette machine. Cet ordinateur prend ses instructions et ses données à l'aide de cartes perforées, comme cela était prévu sur la machine de Babbage, et comme le métier à tisser de Jacquard environ deux siècles auparavant. Dans les années 1950, Grace Hopper est motivée par l'idée que l'informatique devrait être accessible à un plus grand nombre de personnes, et pas seulement aux spécialistes des ordinateurs et aux mathématiciens. Elle défend l'idée que les cartes perforées sont un frein au développement de l’informatique et travaille sur un projet de « langage de programmation » qui serait proche de l'anglais, et qui faciliterait l'écriture des programmes. La difficulté est alors de concevoir le programme capable de transformer des instructions de haut niveau (le langage proche de l'anglais et facilement compréhensible par un humain) en instructions de bas niveau (le langage de la machine). Un tel programme est aujourd'hui appelé « compilateur » et c'est en partie à Grace Hopper que nous en devons l'invention. Son langage de programmation, appelé COBOL, sera le plus utilisé entre 1960 et 1980.

Grace Hopper n'est pas célèbre uniquement pour avoir rendu les ordinateurs plus accessibles aux non-spécialistes. Un jour, alors qu'elle programme ses ordinateurs avec des cartes perforées, l'un d'eux tombe en panne. Allant voir ce qui a pu se produire, elle trouve une mite coincée dans un des trous d'une carte perforée. Elle colle alors sur son rapport le morceau de carte avec un commentaire désignant l'insecte comme coupable de la panne. « Insecte » se disant « bug » en Anglais, ce terme a  été utilisé auparavant par les scientifiques, comme Thomas Edison, pour désigner une erreur due à l'intervention indésirée d'une de ces petites bêtes dans leurs expériences. En l'appliquant à l'exécution échouée d'un programme informatique, Grace en a fait le terme le plus utilisé pour qualifier cette situation.

Découverte d’un « bug » (insecte) par Grace Hooper, en 1947