Eclairage scientifique – Signal vs information
1, 2, 3, codez ! - Eclairage scientifique - Signal vs information
Du
latin signum (« signe convenu »), le signal est un porteur
(ou vecteur) d’information. L’information est portée par les
fluctuations d’une grandeur (physique, le plus souvent) générées par un
phénomène (naturel ou technologique).
On peut classer les signaux de nombreuses façons, comme par exemple :
Type de signal |
Support physique |
|
Signal analogique : vecteur physique à évolution continue, en amplitude et dans le temps |
Signal sonore : le vecteur est une onde de compression (sonnerie, tambour…) |
Pour interpréter correctement un signal (et donc décoder l’information qu’il porte), émetteur et récepteur doivent préalablement choisir une convention commune . Mais malgré cette évidente connivence, il faut traiter le signal pour l’utiliser. L’appellation « traitement du signal » est cependant assez vague, car elle recoupe de nombreux aspects :
- La discrétisation d’un signal analogique pour
faciliter sa manipulation (en particulier sa numérisation sur un support
digital). La discrétisation suppose à la fois de découper le signal en
un nombre fini de valeurs à intervalles réguliers (de temps ou
d'espace), puis de représenter chaque valeur de manière approchée pour
que toutes se trouvent dans un ensemble fini de valeurs possibles.
Enfin, on encode ces valeurs, par exemple en binaire, pour les
représenter dans la machine.
On différencie parfois la discrétisation spatiale (qu’on appelle « pixellisation »), la discrétisation d’amplitude (« quantification ») ou temporelle (« échantillonnage »). Cependant, il est courant d’employer, par abus de langage, le terme « échantillonnage » pour ces 3 aspects : dans tous les cas, on prélève périodiquement des échantillons du signal.
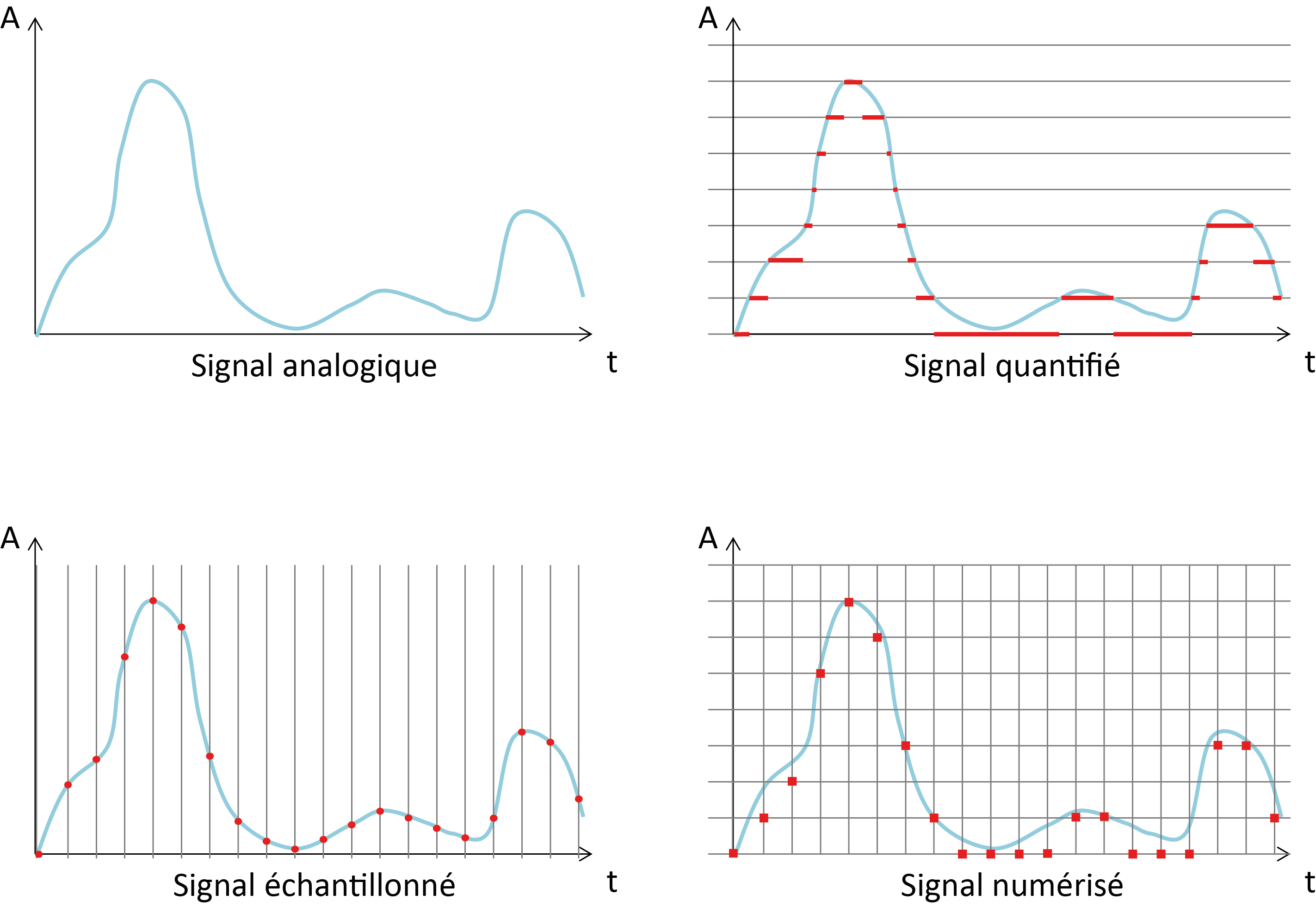
Etapes de discrétisation (en rouge) d’un signal analogique (en bleu).
- La compression du signal pour son stockage et sa transmission (plus le message est long, plus il y a de risques d’introduire des erreurs lors de l’émission, de la transmission, de la réception, du stockage, ou de l’interprétation du signal). Les méthodes de compression peuvent s’effectuer soit avec, soit sans pertes : l’usage final dictera laquelle choisir. Le choix de la compression avec ou sans perte dépend bien de l'usage final, mais aussi du type d'information (sur une image ce peut être acceptable, mais pas sur du texte) et de l'espace de stockage/temps de transmission disponible. C'est donc un compromis.
- L’amélioration de sa qualité : on cherche souvent à séparer l’information (pertinente) du bruit (parasite) inhérent à tout phénomène physique. Pourtant il n’existe pas de définition absolue du bruit : par exemple le bruit de fond détecté par Penzias et Wilson en 1964 qui perturbait les échanges radio du laboratoire Bell s’est avéré être la signature du Big Bang recherchée par les astronomes (le fameux « fond diffus cosmologique », dont la découverte leur a valu le prix Nobel). On caractérise souvent la « qualité » d’un signal par un nombre appelé « rapport signal/bruit ».
- L’interprétation : il s’agit ici d’extraire l’information pertinente, au regard de l’usage que l’on veut en faire : par exemple, sur un feu de signalisation, c’est la couleur (rouge, vert, orange) qui nous importe, et pas l’intensité du flux lumineux émis par la lampe.
Théories de l’information (Shannon vs Kolmogorov)
La numérisation de l’information a engendré de nouvelles disciplines, portées en particulier par Shannon et Kolmogorov.
Claude Elwood Shannon (dont nous avons fêté en 2016 le centenaire de la
naissance) est un ingénieur en génie électrique et un mathématicien
américain. En parallèle de ses recherches au Massachussetts Institute of Technology
(MIT), il travaille aux laboratoires Bell où il décrit la communication
entre machines, introduisant le schéma désormais classique
« source -> encodeur -> signal -> décodeur ->
destinataire ». En 1948, Shannon (avec l’aide de son collègue
Weaver) initie la « théorie mathématique de la communication de
l’information » (TMCI, que la postérité a simplifiée en
« théorie de l’information »). Il décrit précisément dans un
signal ce qui tient de l’information, de la redondance (le surplus) et du bruit
(les intrus), afin d’améliorer la communication. L’idée est de limiter
la redondance pour que, malgré le bruit, l'information soit préservée,
tout en ayant un message le plus court possible.
La notion de redondance peut s’illustrer facilement
en linguistique : dans une phrase, le sens vient de l’agencement et
du choix des mots, pas seulement des lettres et des syllabes qui le
constituent… En effet, « ctt phrs rst prftmnt cmprhnsbl »
(cette phrase reste parfaitement compréhensible) : en limitant les
redondances, on diminue la taille du message.
Le bruit est une dégradation du signal imposée par les contraintes
physiques inhérentes à la communication : l’information est au
mieux brouillée, au pire perdue (dans ce cas, les redondances peuvent
contrer l’impact du bruit en offrant des pistes intéressantes pour la
correction des erreurs). À ce titre, Shannon a démontré que, pour
s’assurer de la qualité de la numérisation, il faut que
l’échantillonnage adopte un « pas » deux fois plus petit que
le motif le plus petit de l’information.
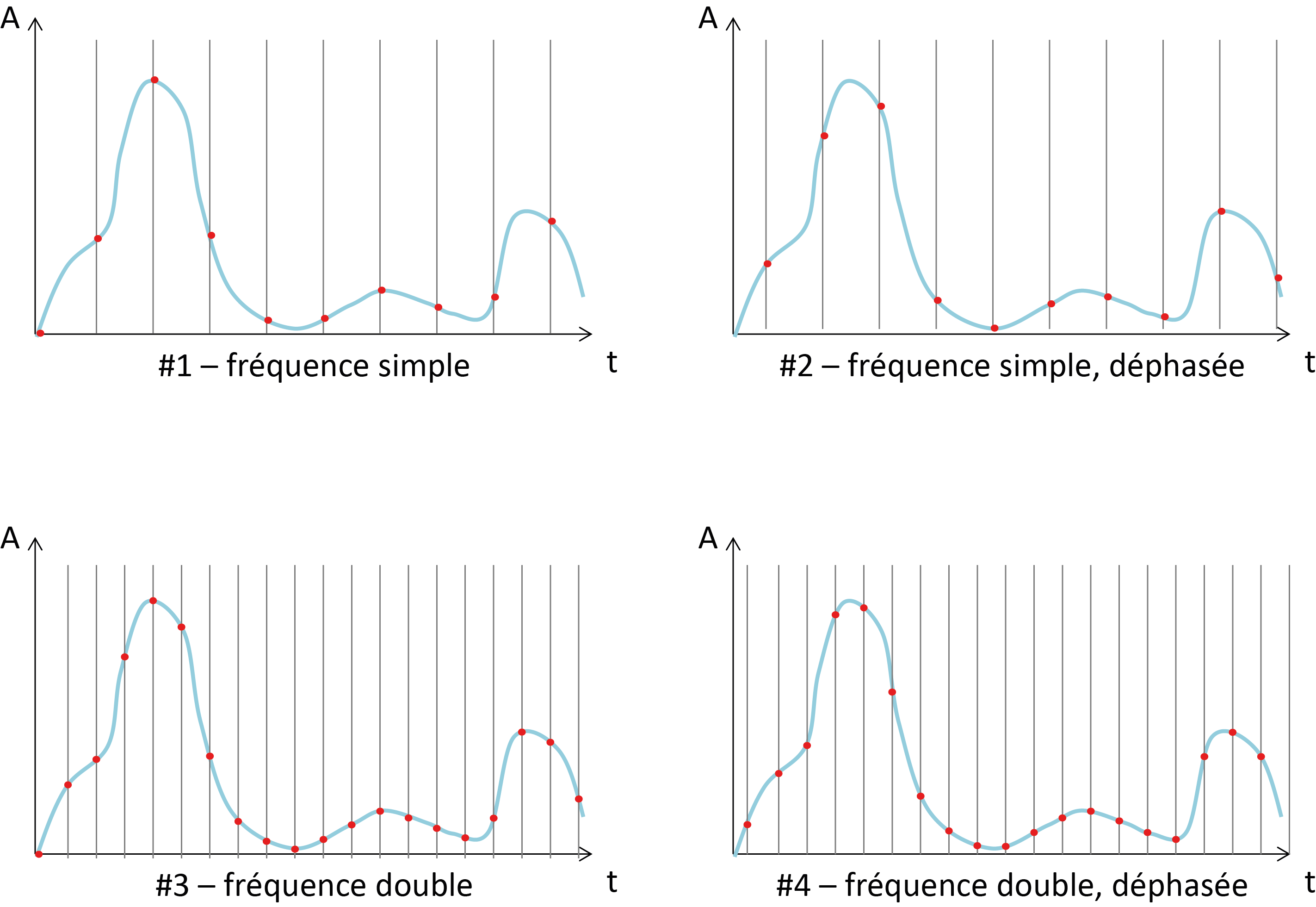
Illustration du théorème de Shannon : avec un échantillonnage
de la même taille que les motifs à reproduire (#1 et #2), il est
possible de sous-estimer grandement les pics selon le centrage des
échantillons (l’épaulement initial manque en #1, le pic principal est
tronqué en #2) ; par contre, avec une fréquence d’échantillonnage
double (#3 et #4), quel que soit le centrage des échantillons, tous les
pics sont toujours bien représentés.
Le théorème de Shannon peut également être utilisé pour distinguer bruit et information. En prenant l’exemple d’une image à l’écran, si un pixel montre une information différente de celle des pixels environnants, c’est probablement un bruit ; si deux pixels contigus ont le même comportement dans un environnement distinct, alors il s’agit probablement d’un vrai motif.
Dans les années 1960, le mathématicien russe Andreï Nikolaïevitch Kolmogorov (aidé de ses collègues Solomonov et Chaitin) propose une approche différente de la TMCI de Shannon : la « théorie algorithmique de l’information ». Cette théorie vise à quantifier et qualifier le contenu en information d’un ensemble de données, sa « complexité ». Prenons par exemple ces quatre descriptions du blason provençal ci-contre :
|
|
La description #1 semble la plus courte de toutes (la
moins complexe), mais elle est ambigüe (trop de blasons différents
correspondent à ce descriptif). La description #2 est réservée aux
connaisseurs : seuls les héraldistes savent l’interpréter
« correctement » ; à vrai dire, ils ne peuvent peut-être
pas reproduire à l’identique ce blason, mais l’information pertinente
pour eux réside dans le nombre, la couleur et l’agencement des figures,
pas dans leur taille précise au centimètre près.
La description #3 est très précise, mais très longue : elle est
assurément plus complexe que la description #1, et reproduit fidèlement
le motif initial. La description #4 reproduit un motif identique au cas
#3, mais avec moins de mots : l’information en est aussi complexe,
donc ; inversement, la seule longueur de la description ne suffit
pas à décréter si l’objet en question est complexe ou pas. On retrouve
par contre dans cet exemple #4 l’origine du nom de cette théorie :
on a recherché l’algorithme le plus simple qui permette de reproduire à
l’identique le motif initial. Et c’est donc en comparant la complexité
de ces différents algorithmes que l’on peut commencer à classer la
complexité des informations.
Parfois, l’émetteur est un système naturel (exemple : une étoile) et ne peut donc pas « choisir » une convention avec le récepteur, humain. C’est alors le travail du scientifique de modéliser le fonctionnement de cette étoile pour comprendre quel état physique est associé à quel signal émis.
Extrait de "1, 2, 3... codez !", Editions Le Pommier, 2016-2017. Publié sous licence CC by-nc-nd 3.0.

