Situation déclenchante

Le professeur évoque le débat sociétal actuel autour de la confidentialité des échanges (écoutes téléphoniques, surveillance d’Internet…) et replace ce débat dans un contexte historique plus large : les hommes ont toujours voulu protéger leurs communications (pour envoyer des lettres amoureuses, des ordres militaires, ou des informations diplomatiques…) tandis qu’ils ont, en parallèle, toujours voulu percer les secrets de leurs voisins et/ou ennemis.
Le professeur demande aux élèves de prendre 5 minutes pour écrire ce à quoi leur fait penser le mot « cryptographie ». Il met en commun leurs propositions au tableau. Quelques exemples de réponses fréquentes au cycle 4 : cryptogramme, informatique, algorithme, crypter, décrypter, coder, décoder, pirater, nombre premier, CB, robot, sécurité, protection des données…
Il propose ensuite aux élèves un défi simple : comment écrire un message, par exemple un SMS, à un ami sans que ce message puisse être compris par d’autres personnes (en particulier, les parents, les professeurs, etc.).
La discussion collective fait ressortir le besoin, pour l’émetteur du message et son destinataire, de se mettre d’accord sur un « code » (on précisera le vocabulaire plus tard).

Recherche (par groupes)

Les élèves, répartis par petits groupes (4 élèves, par exemple), doivent réfléchir à un code leur permettant de communiquer secrètement. Ils doivent expliciter leur méthode et l’agrémenter d’un exemple avec une question et une réponse.
Note : pour plus de simplicité, on ne cherche pas à différencier les majuscules et les minuscules, et on ignore les caractères accentués.

Mise en commun

Le professeur organise une mise en commun au cours de laquelle les différents binômes présentent leurs propositions, qui sont discutées collectivement. On cherche à savoir, par exemple, si le « code » :

•  permet de communiquer (les 2 protagonistes se comprennent-ils ? y a-t-il des ambiguïtés ?) ;
•  est facile à apprendre et à utiliser ;
•  est difficile à « casser » pour une personne extérieure qui ne connaîtrait pas ce code.

Exemples de proposition d’élèves :

•  Mélanger l’ordre des lettres du message : écrire de droite à gauche, écrire en « verlan », écriture « miroir » (dans laquelle l’ordre, mais aussi la forme des lettres, est inversée). Si cette proposition apparait, distribuer des miroirs aux élèves pour qu’ils puissent manipuler.
•  Cacher le message à l’intérieur d’un autre : écriture en dent de scie…
•  Supprimer certains caractères (par exemple les voyelles).
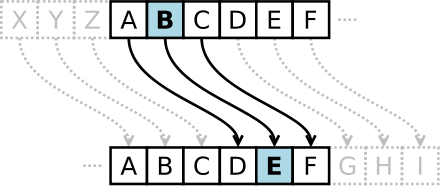
•  Remplacer les lettres du message par des chiffres (A →01, B → 02…). Attention, si on remplace simplement A par « 1 », le chiffrement est facile, mais le déchiffrement est ambigu : « 13 » signifie-t-il « 1 » puis « 3 », c’est-à-dire A puis C, ou la treizième lettre, c’est-à-dire  M ? Pour lever l’ambiguïté, il faut utiliser 2 chiffres pour chaque lettre.
•  Remplacer les lettres par des symboles non chiffrés, comme dans le code morse (traits, points, espaces…)
•  Utiliser une langue étrangère peu répandue (le navajo, par exemple).
•  Utiliser une langue que l’on invente pour les besoins de notre communication. Ce ne sont pas les lettres qui sont remplacées par des chiffres ou autres symboles, mais des mots qui sont remplacés par d’autres.
•  Parler dans sa propre langue, mais en supprimant les espaces, les caractères accentués et la ponctuation.

Si certaines de ces propositions ne sont pas faites par les élèves, ne pas les introduire maintenant : ce sera fait plus tard dans la séance.

Note pédagogique
Au cours de cette discussion, quelques éléments de vocabulaire sont précisés :

•  « Crypter » un message signifie le brouiller pour que son contenu ne soit compréhensible que par son destinataire. Le message n’a donc pas besoin d’être caché. Cette activité s’appelle la cryptographie (on utilise les verbes « crypter » et « décrypter »). La cryptanalyse consiste à trouver la méthode permettant de décrypter un message qui ne nous est pas destiné.
  •  Lorsque les mots sont échangés avec d’autres mots ou expressions (exemple : « Jupiter » désigne le professeur de mathématiques), ce cryptage s’appelle un « code ». On utilise les verbes « coder » et « décoder ».
  •  Lorsque ce sont les lettres qui sont remplacées (et non les mots), soit par d’autres lettres, soit par d’autres types de signes, on parle de « chiffrement ». On utilise les verbes « chiffrer » et « déchiffrer ».
•  On peut aussi chercher à cacher le message, plutôt qu’à le rendre inintelligible. Dans ce cas, le message est transmis « en clair », mais c’est le support du message qui est caché (par exemple, un bout de papier roulé dans un stylo…). Cette activité s’appelle la stéganographie. Elle a été très utilisée dans l’antiquité et peut faire l’objet de séances spécifiques (cf. « prolongements » proposés à la fin de cette séance).
•  Certaines propositions des élèves (comme le code morse) ne relèvent ni de la cryptographie ni de la stéganographie. Il ne s’agit pas de cacher le message ou de le rendre confidentiel, mais simplement de lui trouver un support qui soit pratique. Le morse associe des lettres à des impulsions électriques plus ou moins brèves car c’est un moyen commode de communiquer par le télégramme. Le morse peut être un bon moyen d’étudier l’encodage de l’information, mais pas la cryptographie.

Exercices

Le professeur distribue la Fiche 1 à chaque élève. Cette fiche présente plusieurs messages cryptés (chiffrés ou codés) par des méthodes différentes. Les élèves doivent retrouver le message clair.

La Fiche 2 fournit une table de correspondance permettant de faciliter le travail de l’exercice 3. Le professeur la distribue, ou non, selon l’aisance des élèves dans cet exercice.

Les exercices sont corrigés collectivement.

•  Exercice 1 : il s’agit d’une simple écriture miroir (de droite à gauche)
   Message crypté :    SERTTEL SEL RESREVNI D TIFFUS LI
   Message clair :        IL SUFFIT D INVERSER LES LETTRES
•  Exercice 2 : même chose, mais la suppression des espaces rend le message plus difficile à saisir
   Message crypté :            RUDSULPTSECSECAPSESELSNAS
   Message clair, sans les espaces :      SANSLESESPACESCESTPLUSDUR
   Message clair, avec les espaces :    SANS LES ESPACES C EST PLUS DUR
•  Exercice 3 : il s’agit d’une simple correspondance entre les lettres et leur rang dans l’alphabet (A →01, B → 02…)
   Message crypté :        1511202103151414010919120112160801020520
   Message clair :            OKTUCONNAISLALPHABET
   Message clair avec les espaces : OK TU CONNAIS L ALPHABET    

L’exercice 3 permet de constater que chiffrer l’alphabet à l’aide de nombres à 2 chiffres laisse la possibilité de chiffrer d’autres caractères (minuscules, caractères accentués…) car seuls 26 nombres ont été utilisés, sur un total de 100 nombres possibles (de 00 à 99).

Conclusion

Le professeur fait remarquer un point commun à toutes les méthodes de cryptage (codage ou chiffrement) étudiées ici : passer du texte clair au texte crypté nécessite le même type d’opération que de passer du texte crypté au texte clair. Il peut préciser que ce n’est pas toujours le cas (cf. Séance 5).
La classe définit collectivement les concepts-clés cités dans l’en-tête de cette séance : cryptographie, cryptanalyse, chiffrement, stéganographie et algorithme.

Prolongements EPI

•  En français : étude du rôle de la ponctuation dans la compréhension d’un texte.
•  En mathématiques : l’encodage (code morse, ASCII, binaire…)
  La classe peut étudier comment l’information peut être encodée de façon à pouvoir être stockée et transmise facilement. Le morse offre un bon exemple historique, l’ASCII et le binaire sont plus en phase avec l’informatique d’aujourd’hui.
•  En physique-chimie, et en mathématiques : stéganographie
  Notre projet traite de façon approfondie la problématique du chiffrement. La classe peut le prolonger en ajoutant quelques séances de mathématiques et/ou de physique-chimie pour étudier la stéganographie.
  •  En physique-chimie : fabriquer de l’encre « sympathique » (avec du lait ou du jus de citron : le message se révèle à la chaleur)
  •  En mathématiques : cacher une information à l’intérieur d’une image (format pbm). Cela nécessite 3 à 4 séances, car les élèves doivent d’abord travailler sur la représentation d’une image (encodage des pixels) ainsi que sur l’encodage des textes en ASCII et en binaire. Une fois ces compétences acquises, on peut encoder un message dans la parité des pixels d’une image en niveau de gris, par exemple (256 niveaux de gris sont suffisants). À l’œil, on ne remarque rien, tandis qu’en ouvrant l’image dans un éditeur de texte, on peut récupérer l’information cachée (après un décodage binaire→ ASCII).