Situation initiale

Le professeur demande à 2 élèves de refaire une démonstration à la classe de la méthode d’échange des clés vue à la séance précédente.

Il demande alors aux élèves si ceux-ci peuvent identifier le point faible de cet échange. Si les élèves ne trouvent pas par eux-mêmes, il les guide en leur demandant ce qui se passe si Ève (qui tente de percer le secret de la correspondance entre Alice et Bob) intercepte le premier message (étape 2, ci-avant).
Si ça n’est pas Bob qui reçoit le message, mais Ève, alors Ève peut se faire passer pour Bob, sans que lui-même le sache (il ne saura même pas qu’Alice a tenté de communiquer avec lui). Ève, usurpant l’identité de Bob, pose son propre cadenas et le renvoie à Alice. Alice, pensant recevoir la réponse de Bob, retire son cadenas. À l’étape suivante, Ève reçoit le message et peut le déchiffrer. On peut illustrer cette interception comme cela :

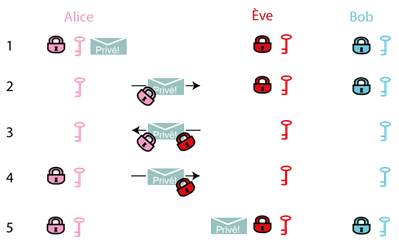
Ainsi, l’utilisation d’une double clé privée permet de communiquer secrètement sans avoir besoin d’échanger sa clé, mais ne résiste pas à l’interception par un tiers. Et ceci pour une raison simple : aucun interlocuteur ne peut vérifier l’identité de l’autre. Rappelons que l’utilisateur, quel qu’il soit, ne « voit » pas les cadenas (ni leur couleur), mais simplement une chaine de caractère chiffrée, qui ressemble beaucoup à un texte aléatoire.

Introduction de la clé publique (collectivement)

Le professeur explique que cette méthode se résout en introduisant 2 clés pour chaque personne, une clé publique (que tout le monde peut connaître) et une clé privée. Le point important est que ces 2 clés ne permettent pas de faire la même chose :

•  La clé publique permet uniquement de chiffrer le message ;
•  La clé privée permet, seule, de le déchiffrer.

Cette méthode nécessite, en pratique, d’utiliser des fonctions asymétriques (cf. prolongement). Pour notre analogie du cadenas et des clés : la clé publique est similaire au cadenas ouvert (en fermant le cadenas, on chiffre le message), tandis que la clé privée est représentée par la clé du cadenas. Ainsi, Alice et Bob mettent à la disposition de tout le monde leur cadenas, mais pas leur clé.

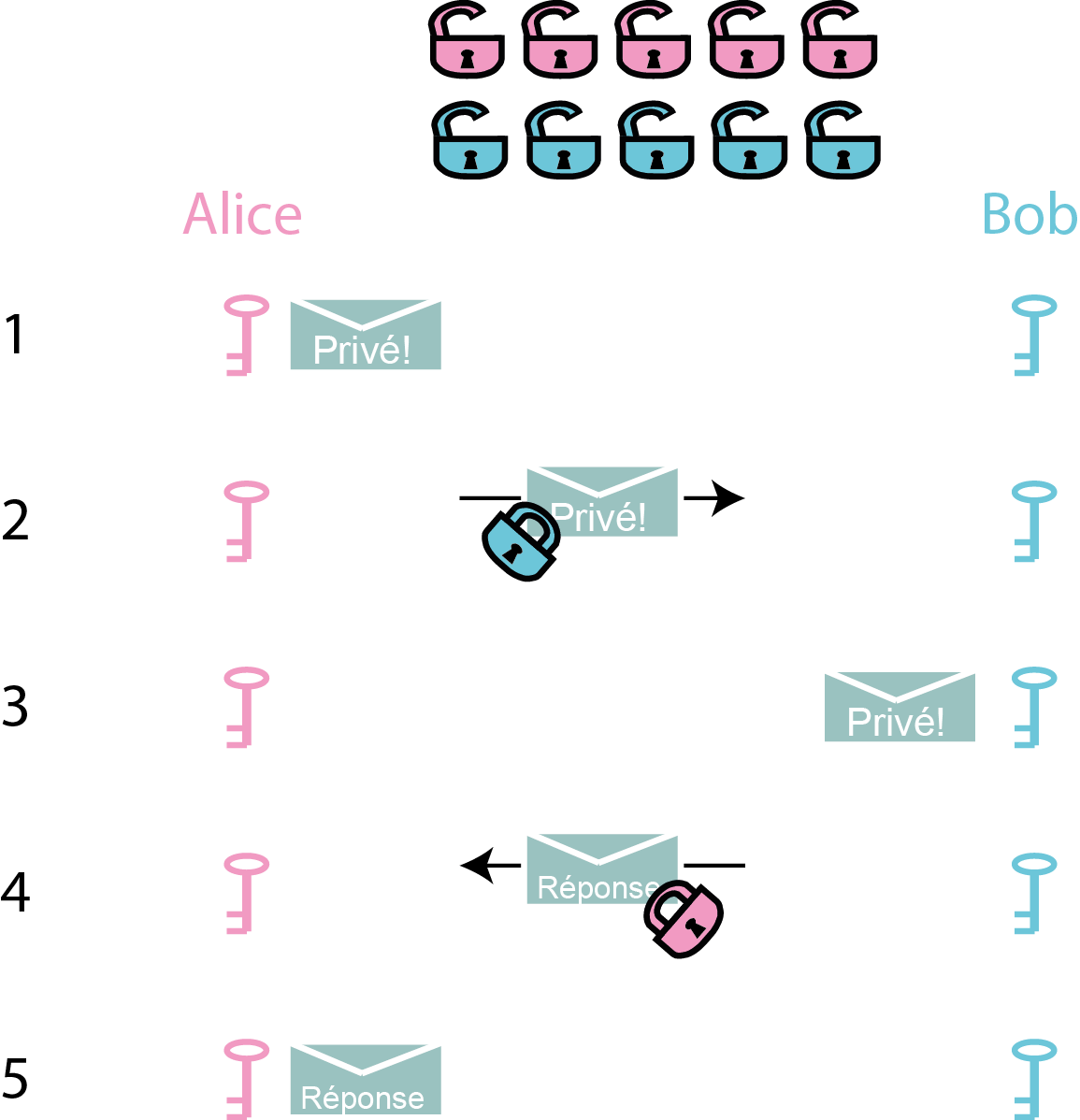
Dans ce cas, Alice envoie simplement son message en utilisant le cadenas de Bob (sa clé publique). Bob est le seul à disposer de la clé permettant de déchiffrer ce message ; il le fait et, s’il souhaite répondre à Alice, il utilise le cadenas d’Alice.
Ève peut intercepter n’importe quel message : puisqu’elle ne dispose pas des clés privées d’Alice ou de Bob, elle ne pourra déchiffrer ni le message original, ni sa réponse.

Exercice

Comme à la séance précédente, les élèves s’exercent quelques minutes à ce chiffrement asymétrique.

Notes scientifiques

•  Le problème avec la solution sans clé publique (cf. séance précédente) est que Alice et Bob ne partagent aucune information, aucun moyen d'identification, et que, du coup, tout ce que Bob peut faire, Ève peut aussi le faire en se faisant passer pour Bob, et Alice n'a pas moyen de savoir si elle communique avec le vrai ou le faux Bob. Avec le système de clé publique/privée, Alice et Bob partagent une information (qu'ils ont eu via une tierce partie de confiance par exemple) : la clé publique de l'autre. Alice sait donc que si elle met le cadenas de Bob sur un message, seul lui pourra le déchiffrer
•  La cryptographie asymétrique permet non seulement de chiffrer (et déchiffrer) des messages, mais aussi de s’identifier. Alice peut chiffrer sa signature avec sa clé privée et tout un chacun peut vérifier (à l’aide de sa clé publique) que la signature est bien celle d’Alice.

Etude documentaire (individuellement)