Ressource

Peut-on dire que la croissance des émissions de CO2 est exponentielle ?

Auteurs : S. Chevillard, M. Olivi, D. Saucez

« Croissance exponentielle », cette expression est abondamment utilisée par les médias pour qualifier la croissance d’un secteur économique, de la consommation d’énergie ou encore de la quantité de déchets produits. Si l’on imagine bien une quantité qui croit vite et fort, la signification exacte de cette notion reste largement méconnue et peu intuitive [1].

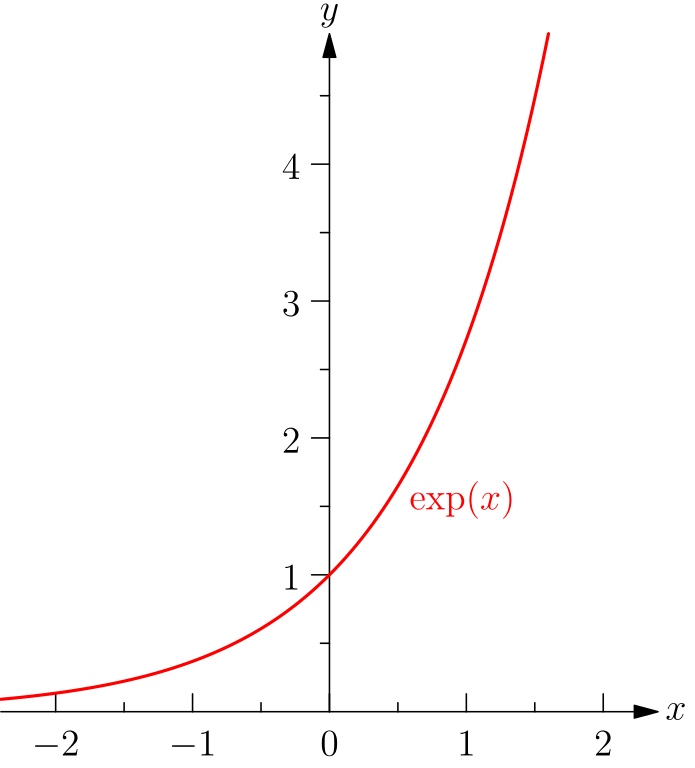
Mfnf-exp — Figure 0 – Graphe de la fonction x → exp(x). Source : Wikimedia Commons

Il nous a donc paru important de mettre à disposition des enseignants des outils et des ressources pour proposer aux élèves une approche concrète de cette notion. Il nous semble qu’ils peuvent être utilisés dès la classe de seconde, même si la notion de fonction exponentielle n’est qu’au programme de première.

Ce texte accompagne un notebook qui a servi de support à un atelier « mathématiques et environnement » pour des élèves de seconde (stage MathC2+/Inria 2022). L’atelier proposait d’analyser des données publiques fournissant une estimation des émissions de carbone chaque année entre 1751 et 2014. Son objectif était de guider les élèves vers une expérience de démarche scientifique :

observer les données ;
élaborer une hypothèse : la croissance exponentielle de la quantité de carbone émise dans l’atmosphère année après année par les activités humaines ;
ajuster ce modèle mathématique sur les données ;
analyser la pertinence et les limites du modèle.

Nous proposons ici quelques réflexions susceptibles de compléter l’atelier en élargissant notre propos à une série de graphiques, publiés par un groupe de chercheurs en science du système Terre [2]. Ces graphiques montrent l’évolution d’un certain nombre d’indicateurs à l’échelle mondiale :

des indicateurs du système Terre, d’une part (concentration de CO2 dans l’atmosphère, température de surface, acidification des océans, etc.) ;
des indicateurs socio-économiques, d’autre part (taille de la population, PIB, etc. ).

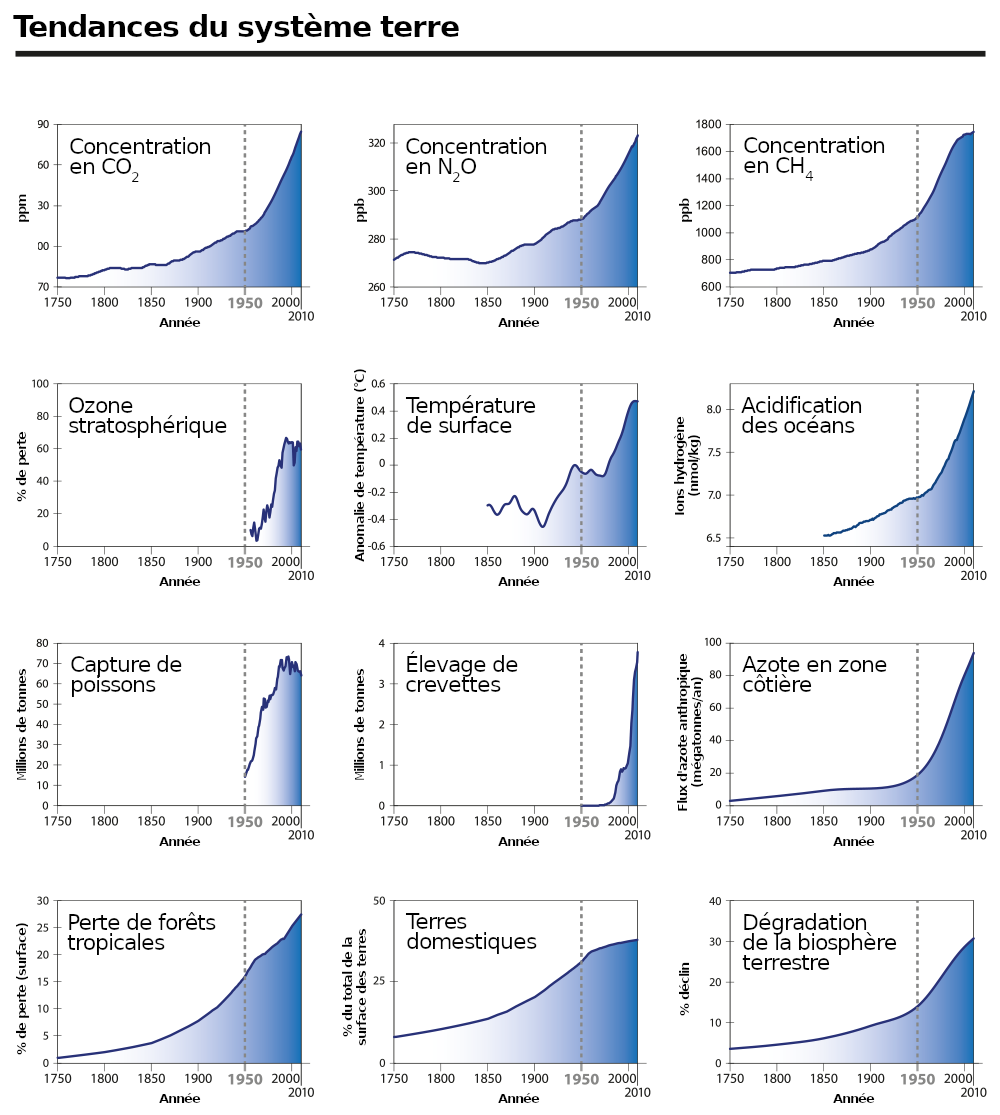
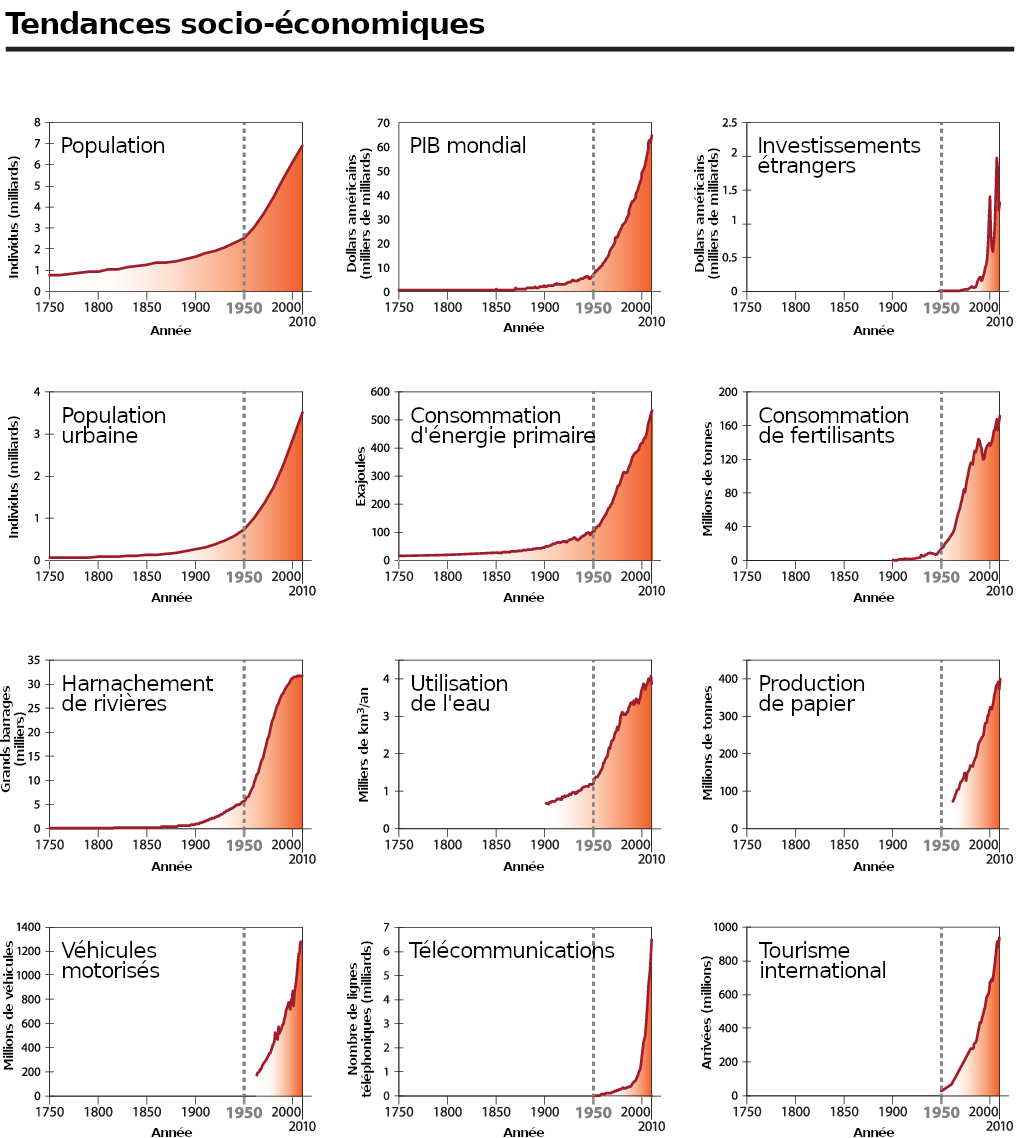
Figure 1 – Évolution au cours du temps de divers indicateurs liés au système Terre.

Figure 2 – Évolution au cours du temps de divers indicateurs traduisant les activités socio-économique humaines.

Il est frappant de constater que la plupart des courbes représentées sur ces graphiques ont une allure semblable, qui rappelle la courbe de la fonction exponentielle (voir figure 0) : elles exhibent une pente légère de 1750 à 1950, puis à partir de 1950 cette pente s’accentue de plus en plus pour devenir quasi verticale sur certains graphiques. L’expression grande accélération a été utilisée pour qualifier ce phénomène.

Les auteurs de ces graphiques avaient pour objectif d’alimenter le débat sur l’Anthropocène, une hypothétique nouvelle époque géologique qui succéderait à l’Holocène et serait marquée par l’influence de l’être humain sur le système Terre. Si les scientifiques s’accordent sur la nécessité d’introduire une nouvelle ère, celle-ci n’a pas encore été officiellement reconnue et la date de début fait débat (celle-ci doit en outre correspondre à un événement majeur à l’échelle du globe, événement enregistré dans les sédiments de manière visible et qui est matérialisé par un clou d’or). Les auteurs des graphiques de la « grande accélération » plaident pour l’année 1950.

Si ceux-ci n’évoquent pas la croissance exponentielle dans leurs travaux, leurs graphiques ont été largement médiatisés en ces termes [3]. Alors, dans quelle mesure peut-on véritablement parler de croissance exponentielle ?

Partir avec de « bonnes » données

Les données sont souvent essentielles à une étude scientifique. Dans les sciences expérimentales, c’est la matière première du chercheur, son lien au monde réel. Si à l’heure de la « numérisation du monde », les données abondent, leur récolte reste une question scientifique centrale pour de multiples raisons :

elles ne sont pas toujours publiques (respect de la vie privée, secret industriel) ;
elles sont parfois inexistantes, ou à tout le moins incomplètes et parfois provenant de sources hétérogènes. Il faut alors bâtir une méthodologie pour combiner les données disponibles ou extrapoler celles qui manquent. On parle alors de données estimées ;
elles ne sont jamais fiables à 100% (erreurs de mesure, d’estimation).

On notera que la précision des données n’a pas la même importance selon le contexte : pour poser une fusée sur la lune, on doit disposer de mesures très précises, mais pour évaluer l’empreinte carbone d’un pays, on peut se contenter d’ordres de grandeur, qui permettent déjà de se faire une idée de l’empreinte relative des différents secteurs [4].

Lorsque les données sont des grandeurs physiques, comme la température ou la concentration de certains composants, il est du ressort du scientifique de concevoir des processus de mesure les plus précis possibles. C’est même l’objet d’une discipline à part entière, la métrologie. Par exemple, le premier graphique de la figure 1, représente l’évolution de la concentration de CO2 dans l’atmosphère au cours du temps. Ces concentrations ont été obtenues, d’une part, à partir de mesures dans des carottes glacières, et d’autre part, pour les périodes récentes, par des mesures directes de l’atmosphère.

Lorsqu’il s’agit de décrire les tendances socio-économiques de la planète, le choix même des indicateurs ne coule pas de source. Parmi les douze indicateurs choisis par les chercheurs dans leur première étude (2004), il y avait le nombre de restaurants McDonald’s retenu comme un indicateur de mondialisation. En 2015, il a été remplacé par l’utilisation d’énergie primaire, « un indicateur clé qui se rapporte directement à l’empreinte humaine sur le fonctionnement du système terrestre » selon les auteurs. Dans cette étude, beaucoup de données ont été estimées et son large périmètre (échelle mondiale, sur deux siècles et demi) rend la tâche très difficile.

Enfin, lorsqu’on utilise des données, il faut s’interroger sur leur provenance et la méthode avec laquelle elles ont été obtenues. La réponse à ces questions doit clairement figurer dans tout article scientifique, comme c’est le cas dans [2]. Lorsque les données sont publiques, cela permet à d’autres chercheurs de vérifier et d’utiliser les résultats présentés. On parle alors de recherche reproductible. Pour s’assurer de la qualité d’un jeu de données, les chercheurs le confrontent à d’autres, testent sa cohérence. De même, lorsque les données ne peuvent pas être rendues publiques, il est tout aussi essentiel de décrire fidèlement le protocole qui a été suivi pour les produire afin de pouvoir attester leur qualité et potentiellement reproduire un jeu de données de manière indépendante.

Dans l’atelier, nous avons utilisé les données publiées sur le site du U.S. Department of Energy.
Il s’agit d’estimations des émissions de CO2 d’origine fossile, de 1750 à aujourd’hui, se basant principalement sur les données de l’Organisation des Nations Unies concernant la consommation de carburant. Les émissions de CO2 provenant de la production de ciment et du torchage des gaz ont également été estimées.

Visualiser et commenter les données

D’un point de vue mathématique, nos données se présentent comme une liste de couples que l’on note (X(n),Y(n)), où n est l’indice dans la liste, X(n) l’année correspondante et Y(n) la valeur correspondante. On peut donc représenter les données dans un repère cartésien, l’année en abscisse et la valeur en ordonnée. Il a été proposé aux élèves d’utiliser la fonction pyplot de la librairie matplotlib de Python.

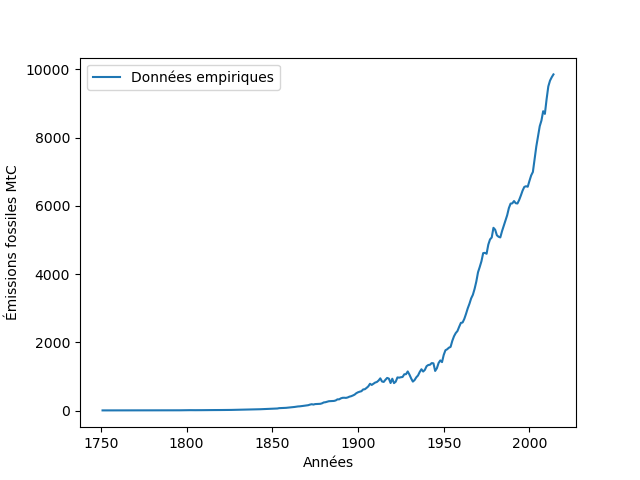
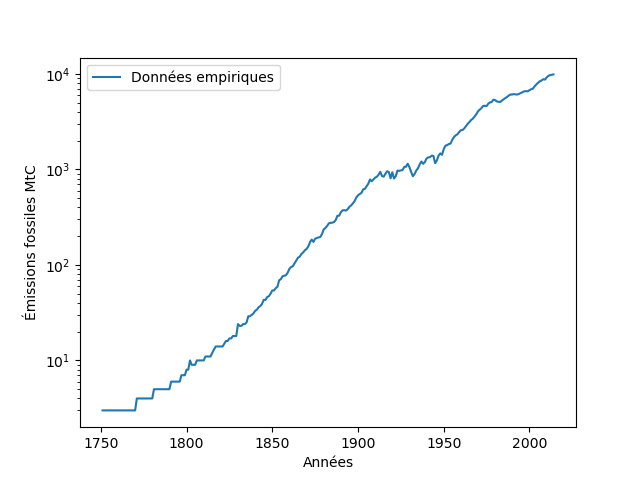
Figure 3a – Représentation de notre jeu de données dans un repère cartésien. La courbe représente les émissions fossiles de CO2 annuelles (exprimées en mégatonnes de carbone, symbole MtC) en fonction de l’année. Exemple : en 1950, l’humanité a émis environ 1600 MtC de CO2.

Dans un graphique, nommer les données, les axes, et préciser les unités est indispensable à la bonne compréhension. Le premier graphique de la figure 1 et celui de la figure 3a représentent tous deux des quantités de CO2 annuelles et, à l’œil, les courbes sont très semblables. Mais on observera que les légendes des axes verticaux diffèrent. Dans le premier, il s’agit de concentrations dans l’atmosphère, mesurées directement ou indirectement (et exprimées en parties par million, symbole ppm) ; dans le second, ce sont des émissions estimées à partir de la consommation de carburants fossiles (et exprimées en MtC). Il ne s’agit pas de la même chose ! Il n’est cependant pas étonnant que ces deux courbes soient si semblables : on sait de façon désormais indiscutable que l’augmentation de la concentration de CO2 dans l’atmosphère est principalement due aux émissions anthropiques (c’est-à-dire, liées aux activités humaines). Pour s’en convaincre, on peut consulter le site [5] et jouer sur l’échelle des temps. Cela n’a pas été fait dans l’atelier, mais on pourrait tracer les deux ensembles de données (émissions et concentrations) sur un même graphique pour comparaison.

On peut aussi tenter d’interpréter le graphique dans un contexte historique. Par exemple, la plus forte pente s’observe entre l’année 1945 et le début des années 70. Cette période, appelée « les trente glorieuses », est caractérisée par un fort développement industriel stimulé par la reconstruction d’après guerre. Il parait logique d’observer une forte croissance des émissions de CO2. Mais toute interprétation étant sujette à débat, cet exercice est surtout destiné à soumettre les commentaires des uns à l’esprit critique des autres. On y voit aussi l’intérêt d’une analyse multidisciplinaire de ce type de données : physiciens du climat, mathématiciens, historiens, sociologues, … sont à même d’apporter des connaissances et des points de vue complémentaires.

À ce stade il est important de faire remarquer que les interprétations graphiques sont toujours à prendre avec beaucoup de précautions. Ainsi, il est essentiel de toujours se poser la question de comment les données sont représentées avant même d’essayer de les interpréter. Par exemple, la figure 3b ci-dessous représente rigoureusement les mêmes données que la figure 3a : la seule différence entre les deux figures est dans la façon de faire progresser les valeurs sur l’axe des ordonnées (échelle linéaire dans le cas de la figure 3a ; échelle logarithmique dans le cas de la figure 3b). Néanmoins, notre intuition aurait tendance à nous faire penser que la progression des valeurs est fondamentalement différente entre les deux figures. Cet exemple est un plaidoyer pour systématiquement expliciter les détails de comment une courbe a été dessinée, en plus d’une description rigoureuse de la source des données elles-mêmes. Aucune analyse ne devrait jamais être effectuée sur la base de courbes dont les axes ne sont pas clairement définis et les données identifiées.

Figure 3b – Représentation du même jeu de données, mais avec l’axe des ordonnées en échelle logarithmique. La façon de représenter les données peut influencer l’intuition et donc fausser leur analyse.

Expérimenter la modélisation mathématique

Les émissions annuelles de CO2 augmentent-elles de manière exponentielle ? Pour répondre à cette question, le scientifique va tenter d’ajuster le modèle mathématique de croissance exponentielle aux données. Ce modèle est défini de la façon suivante : une suite de nombres y(n) suit une croissance exponentielle si, pour passer d’un nombre au suivant, on le multiplie par un nombre constant C [6]. Il s’agit d’une suite géométrique :

y(n+1) = C×y(n).

En comparaison, une suite de nombres y(n) suit une croissance linéaire, lorsque pour passer d’un nombre au suivant on ajoute un nombre constant D. C’est une suite arithmétique :

y(n+1) = y(n)+D.

Ces deux modèles sont particulièrement intéressants du fait de leur simplicité : ils permettent de capturer toute l’information contenue dans une liste grâce à seulement deux nombres : une valeur de la liste, y(0) par exemple, et la constante de croissance
(C ou D suivant le modèle ; on l’appelle la « raison » de la suite). Le prix à payer est qu’un tel modèle ne s’ajuste pas très précisément aux données : sa représentation graphique ne suit pas exactement la courbe des données mais s’en approche suffisamment pour bien décrire la tendance générale.

Afin d’ajuster un modèle exponentiel sur nos données, il faut déterminer le paramètre du modèle, le nombre C. Il existe des méthodes plus sophistiquées pour le faire, mais la méthode la plus simple donne déjà des résultats satisfaisants : il suffit de calculer le nombre C à partir d’une valeur initiale et d’une valeur finale (voir le notebook pour la formule donnant C. On l’a fait sur plusieurs périodes : sur la totalité de l’échantillon [1751, 2014], sur la période des trente glorieuses [1945, 1973] et sur la période du début de la révolution industrielle à la première guerre mondiale [1850, 1913].

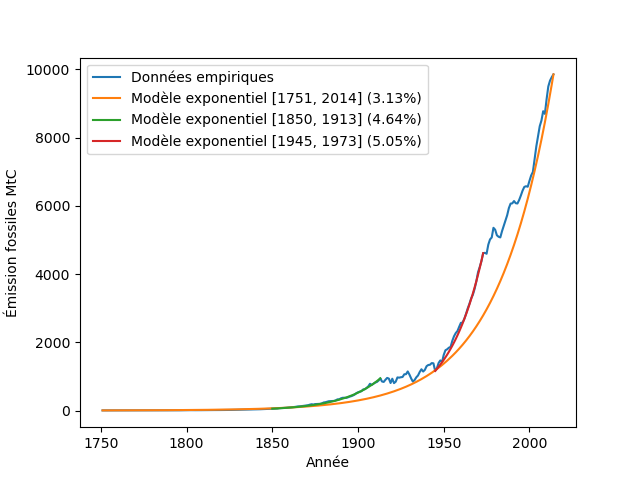
Figure 4 – Superposition des données empiriques et de trois modèles exponentiels dont le paramètre a été ajusté pour correspondre aux données sur trois périodes déterminées : toute la période, la révolution industrielle, les trente glorieuses.

Les pourcentages indiqués dans la légende sont les taux de croissance. Un taux de croissance de 5% par an, cela veut dire que la quantité est multipliée par 1,05 chaque année (C=1,05) : les émissions de CO2 ont cru d’environ 5% par an entre 1945 et 1973.

Pour aller plus loin, on peut observer que la suite des logarithmes, ln(y(n)) est arithmétique :

ln(y(n+1)) = ln(y(n))+ln⁡(C).

On peut donc estimer ln(C) en effectuant un ajustement affine par exemple par la méthode des moindres carrés.

On peut se convaincre de la pertinence du modèle en calculant les émissions cumulées de 1751 à 2014 à partir des données, puis à partir du modèle en utilisant la formule qui donne la somme d’une suite géométrique :

S = y(0)+y(1)+…y(N) = y(0) (C^N+1-1)/(C-1),

où N=263 (c’est-à-dire le nombre d’années entre 1751 et 2014) et C=1,0313.

On obtient, dans les deux cas, de l’ordre de 400 gigatonnes de carbone (une gigatonne égale mille mégatonnes).

Explorer le modèle et ses limites

On observe comme prévu que ces modèles sont trop simples pour rendre compte des variations à court terme des données. Toutefois, ils décrivent plutôt bien la tendance générale, en particulier sur les deux périodes plus courtes [1945, 1973] et [1850, 1913], ce qui est normal. Les intervalles de temps sur lesquels un modèle exponentiel s’ajuste quasi-parfaitement sont généralement assez réduits. Le même constat pourrait être fait sur les graphiques de la grande accélération. Contrairement aux modèles déterministes (lois) de la physique, qui permettent de calculer précisément l’évolution future d’un phénomène, ici, le modèle sert à faire des études prospectives basées sur l’hypothèse que les émissions de CO2 vont continuer à ce rythme. Et c’est déjà très intéressant.

La différence entre deux taux de croissance est souvent difficile à interpréter intuitivement, parce que dans la pratique ce sont en général deux valeurs très proches de 1 : les pourcentages faibles peuvent laisser penser que la croissance l’est aussi. C’est oublier que ce taux est multiplicatif et non pas additif : s’il n’y a pas beaucoup de différence entre multiplier une quantité par 1,03 ou par 1,05, c’est une toute autre histoire lorsqu’on répète cette multiplication année après année. Une bonne façon de rendre le phénomène plus concret est de calculer le temps de doublement : c’est le temps T au bout duquel la quantité annuelle d’émissions aura doublé. Un petit calcul montre que le temps de doublement est indépendant de l’année choisie comme année zéro, et il est uniquement fonction du paramètre du modèle : il vaut ln⁡(2)/ln⁡(C). Comme ce n’est généralement pas un nombre entier, on pourra l’arrondir au nombre entier immédiatement supérieur. Pour un taux d’accroissement de 3,13%, le temps de doublement est de 22,49 ans (arrondi à 23 ans); pour un taux de 3% il est de 23,45 ans (arrondi à 24 ans). Une différence de l’ordre de 0,1% sur le taux de croissance induit une année de différence pour le temps de doublement ! Le temps de doublement est réduit à 14 ans pour un taux de croissance de 5%. Ce concept de temps de doublement nous ramène à une expérience connue : celle des puissances de deux dont on sait qu’elles atteignent très vite des nombres gigantesques (voir [6]).
Il permet d’estimer l’ampleur du phénomène et de ses conséquences à l’échelle humaine.

Prenons par exemple un modèle exponentiel avec une croissance annuelle de 3% pour simplifier. Divisons la période totale [1751, 2014] en successions de périodes de 24 ans (le temps de doublement pour un taux d’accroissement de 3%). Il y a onze périodes que nous numérotons de 0 à 10. Pour chaque période n, calculons les émissions cumulées pendant cette période d’après le modèle, et notons la suite obtenue u(n). La suite
u(n) est alors une suite géométrique de raison 2 : cela découle du fait que, chaque année de la période n a vu sa quantité d’émissions de CO2 doubler par rapport à l’année correspondante dans la période n−1.

On peut en déduire que la moitié de l’ensemble des émissions anthropiques a été émise dans le dernier quart de siècle !

En effet, on a u(1) = 2u(0), mais également u(2) = 2u(1) = 4u(0), etc., de sorte que l’ensemble des émissions anthropiques il y a 24 ans était donnée par

u(0) + u(1) + … + u(9) = u(0) + 2u(0) + … + 2⁹u(0) = (1 + 2 + … + 2⁹)u(0).

Or, la somme des n premières puissances de 2 est, à peu de chose près, égale à
2ⁿ:
précisément
1 + 2 + … + 2⁹ = 1 + 2 + 4 + 8 + … + 512 = 1023 = 2¹⁰ – 1 ≈ 2¹⁰.

Donc les émissions de la dernière période, à savoir u(10) = 2 ¹⁰ u(0), sont essentiellement les mêmes que la somme de toutes les émissions qui ont précédé cette période.

Là encore, il ne s’agit pas de calculs rigoureux (le modèle n’est qu’une approximation des données, nous avons arrondi le temps de doublement), mais d’ordres de grandeurs parlants. Ce même calcul montre que, si les émissions se poursuivent à un rythme de l’ordre de 3% par an, nous émettrons autant durant le prochain quart de siècle que tout ce que l’humanité a émis depuis le début de l’ère industrielle jusqu’à aujourd’hui.

Calculons maintenant selon ce même modèle, la suite v(n) constituée des émissions cumulées entre l’année 1751 et l’année n :

v(n) = y(0)+y(1)+ … + y(n).

Le modèle exponentiel possède une propriété remarquable : cette suite v(n) suit à partir d’un certain rang une progression géométrique de même raison que la suite y(n).
En effet, si la suite y(n) suit une progression géométrique de paramètre C, on a pour tout k, y(k) = y(0) × C^k. Alors, la valeur v(n) est la somme d’une suite géométrique, dont on peut montrer qu’elle vaut

v(n) = y(0) × Cⁿ⁺¹-1) ⁄ (C-1).

Si C correspond à un taux de croissance de τ%, c’est-à-dire que C = 1 + τ/100, alors pour n suffisamment grand, 1 devient négligeable devant Cⁿ⁺¹ et on a

v(n) ≈ α C^n,,

ou α est un nombre constant (α = y(0) × C/(C-1) ≈ 100 × y(0)/τ).

On peut en déduire que les émissions cumulées suivent une progression géométrique de même raison que les émissions annuelles.

Ce résultat peut être confronté aux données, en traçant la courbe des données cumulées : pour chaque année en abscisse, on place en ordonnée la quantité d’émissions cumulées depuis 1751 jusqu’à l’année en question. Puis, on peut ajuster un modèle exponentiel à partir de l’année 1900 par exemple, un choix qui garantit que notre approximation est valide (le modèle nous dit que c’est seulement à partir d’un certain rang que les émissions cumulées suivent une progression géométrique de même raison que les émissions annuelles). Il est très facile de réaliser ce calcul avec les outils du notebook :

Y_cum = [sum(Y[0:n+1]) for n in range(len(Y))]
debut = 1900; fin = X[len(X)-1]
_, _, Y_cum_modele, taux = parametresModeleExponentielPeriode(X, Y_cum, debut, fin)

On obtient un taux de croissance de 3,11% pour les émissions cumulées, sur la période 1900-2014, très proche du taux de croissance que nous avions trouvé pour les émissions annuelles (non cumulées). On peut voir sur la figure 5 que ce modèle s’ajuste très bien aux données. Et donc, les émissions cumulées doublent elles aussi tous les 24 ans. On peut aussi observer un fait bien connu : les émissions cumulées suivent une courbe beaucoup plus lisses que les émissions annuelles.

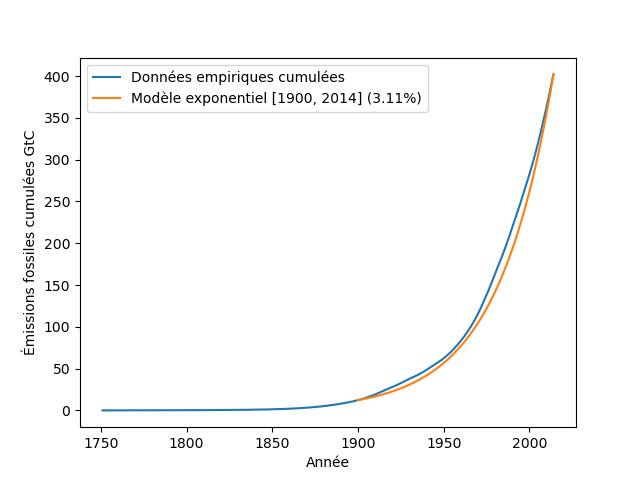
Figure 5 – Superposition des émissions cumulées obtenues à partir des données empiriques et d’un modèle exponentiel dont le paramètre a été ajusté pour correspondre aux données sur la période de 1900 à nos jours.

Ainsi, ce modèle permet de prendre conscience que dans un monde fini, la croissance exponentielle ne peut se poursuivre indéfiniment [8]. Sur quelques graphiques de la grande accélération, on observe un ralentissement ou une stagnation de la croissance. C’est le cas des captures de poissons marins depuis la fin des années 80, qui s’explique vraisemblablement par l’épuisement des ressources. C’est aussi le cas de la construction de nouveaux grands barrages, limitée par le nombre de grands fleuves. Un phénomène qui suit initialement une croissance exponentielle a souvent un tel comportement lorsqu’il commence à se confronter à des limites. Le modèle le plus simple imaginé par le mathématicien belge Pierre-François Verhulst pour décrire cette situation est le modèle logistique [7].

Lexique

Indicateur : outil d’évaluation et d’aide à la décision, élaboré à partir d’un élément mesurable ou appréciable permettant de considérer l’évolution d’un processus par rapport à une référence. (Source : Wikipédia)

Ordre de grandeur : un ordre de grandeur est un nombre qui représente de façon simplifiée mais approximative la mesure d’une grandeur physique. (Source : Wikipédia)

Modèle mathématique : représentation d’un système, biologique ou autre, par un ensemble de variables et de relations mathématiques entre ces variables, comme des équations différentielles. Un modèle simplifie, par définition, la réalité, mais préserve les aspects importants pour étudier un phénomène donné. (Source : Interstice)